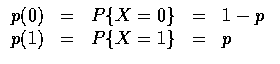
The Bernoulli and Binomial Random Variables
假設進行一試驗, 其結果可區分為 "成功" 和 "失敗", 若令 X=1表示結果是成功, X=0 表示結果是失敗, 則 X 的機率質量函數為
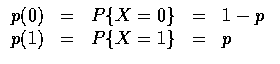
現在假設進行 n 次的獨立試驗, 且每次"成功"的機率均為 p , "失敗"
的機率均為 1-p, 若以 X 表示在 n 次試驗中成功的次數,
則稱 X 為參數是 (n,p) 的二項(binomial)隨機變數.
而 Bernouli 隨機變數就是參數為(1,p)的二項隨機變數.
參數為 (n,p) 之二項隨機變數的機率質量函數為
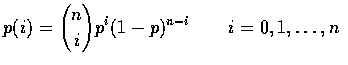
Proof:
考慮任一含有 i 次成功 , n-i次失敗的序列. 由獨立試驗的假設,
我們知道每一這種序列出現的機率均為
pi(1-p)n-i.
又這種序列共有
![]() 種, 故上式得證.
種, 故上式得證.
![]()
由二項式定理,我們可得機率的和為 1, 亦即
![$\displaystyle\sum_{i=0}^n p(i)=\sum_{i=0}^n{n\choose i}p^i(1-p)^{n-i}=[p+(1-p)]^n=1$](img7.gif)