假設有 N 種不同類型的優待券,
且假設某人每次收集到的優待券其類型不但獨立於先前的收集品,
且它是 N 種不同類型中任一種的機會是均等的.
我們有興趣的隨機變數 T 是表示某人在獲得一整套優待券 (即每種類型至少有一張)
時所需收集之優待券的張數. 與其直接計算
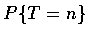 ,
不如讓我們從 T 大於 n 的機率著手. 欲如此做, 首先固定 n,
且定義事件
A1,A2,...,AN 如下:
Aj 為首 n 張優待券中沒有第 j 種類型優待券的事件,
j=1,2,...,N. 因此
現在, 當首 n 張優待券中沒有類型 j 時, 事件 Aj 將發生.
因任一張優待券不是類型 j 的機率為 (N-1)/N,
所以由連續優待券之類型為獨立事件的假設, 我們得
同樣, 當首 n 張優待券中沒有類型 j1 和類型 j2 的優待券時, 事件
Aj1Aj2 發生. 所以再由獨立性的假設得
同理可得
因此, 對 n>0, 得
,
不如讓我們從 T 大於 n 的機率著手. 欲如此做, 首先固定 n,
且定義事件
A1,A2,...,AN 如下:
Aj 為首 n 張優待券中沒有第 j 種類型優待券的事件,
j=1,2,...,N. 因此
現在, 當首 n 張優待券中沒有類型 j 時, 事件 Aj 將發生.
因任一張優待券不是類型 j 的機率為 (N-1)/N,
所以由連續優待券之類型為獨立事件的假設, 我們得
同樣, 當首 n 張優待券中沒有類型 j1 和類型 j2 的優待券時, 事件
Aj1Aj2 發生. 所以再由獨立性的假設得
同理可得
因此, 對 n>0, 得
T 等於 n 的機率可由上面的結果和下面的等式求得:

或
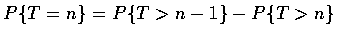
另一個有興趣的隨機變數是首 n 張收集品中不同類型之優待券的種類數 --
以 Dn 表此隨機變數. 欲求
 ,
首先將我們的注意力集中在某一組 k 種不同類型的集合上,
然後去求此組集合就是構成首 n 張收集品中不同類型之集合的機率.
現在, 為了要得到這種情況, 其充分必要條件是首 n 張優待券中
,
首先將我們的注意力集中在某一組 k 種不同類型的集合上,
然後去求此組集合就是構成首 n 張收集品中不同類型之集合的機率.
現在, 為了要得到這種情況, 其充分必要條件是首 n 張優待券中
A:每一張都是這 k 種類型中的其中一種 ;
B:這 k 種類型中的每一種都有優待券.
因為任一張優待券是這 k 種類型中之一種的機率為
 ,
所以 A 將成立的機率為
,
所以 A 將成立的機率為
 .
又,
給予優待券是所考慮的 k 種類型中之一種,
則很容易可以得知此優待券是這 k 種類型中之任一種的機會是均等的.
因此,給予 A 發生,
B 的條件機率和這 n 張優待券含有此 k 種不同類型之整套優待券的機率是一樣的,
其中每一張優待券是這 k 種類型中之任一種的機會是均等的.
但這正是收集此 k 種不同類型之整套優待券所需之張數小於或等於 n 的機率,
而此機率可用 k 取代上面式中的 N 求得. 因此, 我們得到
.
又,
給予優待券是所考慮的 k 種類型中之一種,
則很容易可以得知此優待券是這 k 種類型中之任一種的機會是均等的.
因此,給予 A 發生,
B 的條件機率和這 n 張優待券含有此 k 種不同類型之整套優待券的機率是一樣的,
其中每一張優待券是這 k 種類型中之任一種的機會是均等的.
但這正是收集此 k 種不同類型之整套優待券所需之張數小於或等於 n 的機率,
而此機率可用 k 取代上面式中的 N 求得. 因此, 我們得到
最後, 因為有
 種選取 k 種不同類型的方法, 我們得到
種選取 k 種不同類型的方法, 我們得到





![]() ,
所以 A 將成立的機率為
,
所以 A 將成立的機率為
 .
又,
給予優待券是所考慮的 k 種類型中之一種,
則很容易可以得知此優待券是這 k 種類型中之任一種的機會是均等的.
因此,給予 A 發生,
B 的條件機率和這 n 張優待券含有此 k 種不同類型之整套優待券的機率是一樣的,
其中每一張優待券是這 k 種類型中之任一種的機會是均等的.
但這正是收集此 k 種不同類型之整套優待券所需之張數小於或等於 n 的機率,
而此機率可用 k 取代上面式中的 N 求得. 因此, 我們得到
.
又,
給予優待券是所考慮的 k 種類型中之一種,
則很容易可以得知此優待券是這 k 種類型中之任一種的機會是均等的.
因此,給予 A 發生,
B 的條件機率和這 n 張優待券含有此 k 種不同類型之整套優待券的機率是一樣的,
其中每一張優待券是這 k 種類型中之任一種的機會是均等的.
但這正是收集此 k 種不同類型之整套優待券所需之張數小於或等於 n 的機率,
而此機率可用 k 取代上面式中的 N 求得. 因此, 我們得到

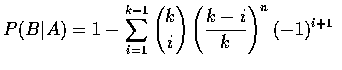
 種選取 k 種不同類型的方法, 我們得到
種選取 k 種不同類型的方法, 我們得到
![$\begin{array}{rcl}
P\{D_n=k\}&=&\displaystyle{N\choose k}P(AB) \\ \\
&=&\displ...
...ight )^n(-1)^{i+1}
\right ] \qquad\rule[0.02em]{1.0mm}{1.5mm}\\ \\
\end{array}$](img15.gif)