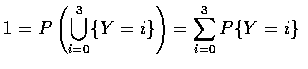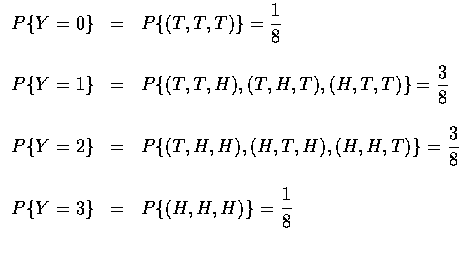
Since Y must take on one of the values 0 through 3, we must have
Random Variables 隨機變數
For instance, in tossing dice we are often interested in the sum of the two dice and are not really concerned about the separate values of the dice. That is, we may be interested in knowing that the sum is 7 are not be concerned over whether the actual outcome was (1,6) or (2,5) or (3,4) or (4,3) or (5,2) or (6,1). Also, in coin-flipping we may be interested in the total number of heads that occur and not care at all about the actual head-tail sequence that results.
Define
These quantities of interest, or more formally, these real-valued functions
defined on the sample sapce, are known as random variables.
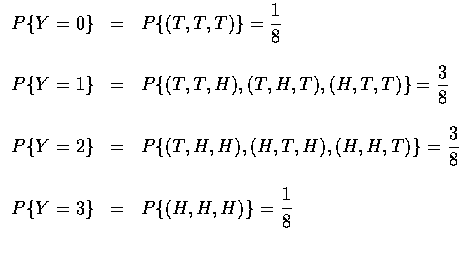
Since Y must take on one of the values 0 through 3, we must have