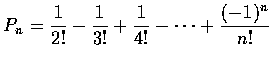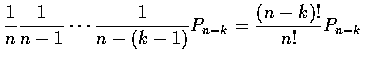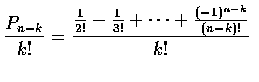The Matching Problem 配對理論
- Example (Matching)
- At a party n men take off their hats. The hats are then mixed up, and each
man randomly selects one. We say that a match mixed up, and each man randomly
selects one. We say that a mathc occurs if a man selects his own hat.
(a) What is probability of no matches?
(b) What is probability of exactly k matches?
- Solution:
- (a)
Let E denote the event that no matches occur, and to make explicit the
dependence on n write Pn=P(E). We start by conditioning on whether or not
the first man selects his own hat -- call these events M and Mc. Then
Pn=P(E)=P(E|M)P(M)+P(E|Mc)P(Mc). Clearly, P(E|M)=0, so
Now, P(E|Mc) is the probability of no matches when n-1 men select from a
set of n-1 hats that does not contain the hat of one of these men. This can
happen in either of two mutually exclusive ways. Either there are no matches
and the extra man does not select the extra hat (this being the hat of the man
that chose first), or there are no matches and the extra man does select the
extra hat. The probability of the first of these events is just Pn-1,
which is seen by regarding the extra hat as "belonging" to the extra man. As
the second event has probability
[1/(n-1)]Pn-2, we have
and thus, from Equation (5.9),
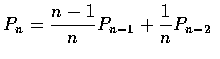
or
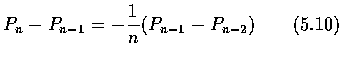
However, as Pn is the probability of no matches when n men select among
their own hats, we have
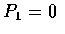 ,
,
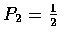 so, from Equation
(5.10),
so, from Equation
(5.10),
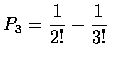 and
and
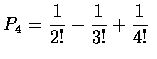 and, in general, we see that
(b)
and, in general, we see that
(b)
To obtain the probability of exactly k matches, we consider any fixed group
of k men. The probability that they, and only they, select their own hats is
where Pn-k is the conditional probability that the other n-k men,
selecting among their own hats, have no matches. As there are
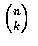 choices of a set of k men, the desired probability of exactly k matches is
choices of a set of k men, the desired probability of exactly k matches is
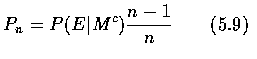
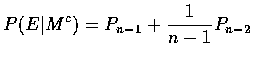
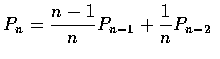 or
or
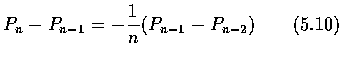
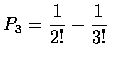 and
and
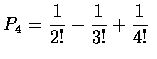 and, in general, we see that
and, in general, we see that