(i)
Let Pn,m the probability that n successes occur before m failures. By conditioning on the outcome of the first trial we obtain:
(ii)
For n successes to occur before m failures, it is necessary and sufficient that there be at least n successes in the first m+n-1 trials. (Even if the game were to end before a total of m+n-1 trials were completed, we could still imagine that the necessary additional trials were performed.) This is true, for if there are at least n successes in the first m+n-1 trials, there could be at most m-1 failures.
On the other hand, if there were fewer than n successes in the first m+n-1trials, there were fewer than n successes in the first m+n-1 trials, there would have to be at least m failures in that same number of trials; thus nsuccesses would not occur before m failures.
Hence, as the probability of exactly k successes in m+n-1 trials is,
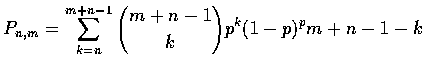
Example
As an illustration of the problem of the points suppose that 2 players each put
up ![]() and each of them has an equal chance of winning each point (p=1/2).
If n points are required to win and the first player has 1 point and the
second none, then the first player is entitled to
and each of them has an equal chance of winning each point (p=1/2).
If n points are required to win and the first player has 1 point and the
second none, then the first player is entitled to
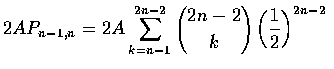
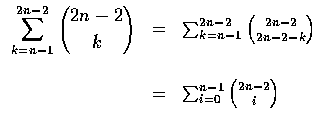
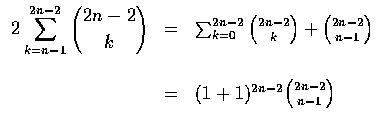
![$\displaystyle A\left [ 1+\left (\frac{1}{2}\right )^{2n-2}{2n-2\choose n-1}\right ]$](img9.gif)