Example
- Example
- An insurance company that believes that people can be divided inot two distinct
classes -- those who are accident prone and those who are not. During any given
year an accident-prone person will have an accident with probability .4, whereas
the corresponding figure for a non-accident-prone person is .2.
(a) If we assume that 30 percent of the population is accident
phone, what is the probability that a new policyholder whill have an accident
within a year of purchasing a policy?
(b) What is the conditional probability that a new policyholder
will have an accident in his or her second year of policy ownership, given that
the policyholder has had an accident in the first year?
[Solution:]
(a)
We shall obtain the desired probability by first conditioning upon whether or
not the policyholder is accident prone. Let A1 denote the event that the
policyholder will have an accident within a year of purchase; and let A denote
the event that the policyholder is accident prone. Hence the desired
probability, P(A1), is given by
(b)
If we let A be the event that the policyholder is accident prone and we let
Ai, i=1,2, be the event that he or she has had an accident in the ith year,
then the desired probability
P(A2|A1) may be obtained by conditioning on
whether or not the policyholder is accident prone, as follows:
P(A2|A1)=P(A2|AA1)P(A|A1)+P(A2|AcA1)P(Ac|A1)
Now,
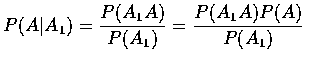
However, P(A) is assumed to equal
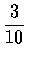 ,
and it was shown in (a)
that
P(A1)=.26. Hence
and thus
Since
P(A2|AA1)=.4 and
P(A2|AcA1)=.2, we see that
,
and it was shown in (a)
that
P(A1)=.26. Hence
and thus
Since
P(A2|AA1)=.4 and
P(A2|AcA1)=.2, we see that
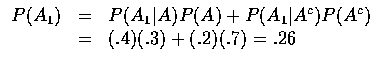
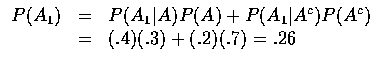
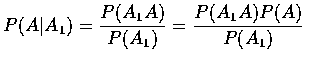
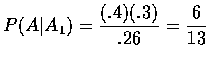
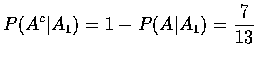
![$\displaystyle P(A_2\vert A_1)=(.4)\frac{6}{13}+(.2)\frac{7}{13}\approx .29\qquad\rule[0.02em]{1.0mm}{1.5mm}$](img7.gif)