Example

Example
重覆投擲兩粒均勻的骰子, 且設每次投擲的結果彼此不互相影響. 試求 在出現點數和為 7 之前出現點數和為 5 的機率.
Solution:
令 En 表示在首 n-1 次試驗中點數和不為 5 也不為 7, 但第 n 次試驗時點數和為 5 的事件, 則所求的機率為
$\displaystyle P\left (\bigcup_{n=1}^\infty E_n\right ) =\sum_{n=1}^\infty P(E_n)$
因 $\displaystyle P\{5 \mbox{on any trial}\}=\frac{4}{36}$, 及 $\displaystyle P\{7 \mbox{on any trial}\}=\frac{6}{36}$, 故由獨立性之假設得
$\displaystyle P(E_n)=\left (1-\frac{10}{36}\right )^{n-1}(\frac{4}{36})$
因此
$\begin{array}{rcl} \displaystyle P\left (\bigcup_{n=1}^\infty E_n\right )&=& \d... ...e\frac{1}{9}\cdot\frac{1}{1-\displaystyle\frac{13}{18}}=\frac{2}{5} \end{array}$

This result may also have been obtained by using conditional probabilities. If we let E be the event that a 5 occurs before a 7, then we can obtain the desired probability, P(E), by conditioning on the outcome of the first trial, as follows: Let F be the event that the first trial results in a 5; let Gbe the event that it results in a 7; and let H be the event that the first trial results in neither a 5 nor a 7. Conditioning on which one of these events occurs gives

P(E)=P(E|F)P(F)+P(E|G)P(G)+P(E|H)P(H)
However,
$\begin{array}{rcl} P(E\vert F)&=&1 \\ P(E\vert G)&=&0 \\ P(E\vert H)&=&P(E) \\ \end{array}$
The first two equalities are obvious. The third follows because, if the first outcome results in neither a 5 nor a 7, then at that point the situation is exactly as when the problem first started; namely, the experimenter will continually roll a pair of fair dice until either a 5 or 7 appears. Furthermore, the trials are independent; therefore, the outcome of the first trial will have no effect on subsequent rolls of dice. Since $\displaystyle P(F)=\frac{4}{36}$, $\displaystyle P(G)=\frac{6}{36}$, $P(H)=\frac{26}{36}$ we see that
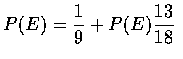$\displaystyle P(E)=\frac{1}{9}+P(E)\frac{13}{18}$ or $P(E)=\frac{2}{5}$
The reader should note that the answer is quite intuitive. That is, since a 5 occurs on any roll with probability $\displaystyle\frac{4}{36}$ and a 7 with probability $\displaystyle\frac{6}{36}$, it seems intuitive that the odds that a 5 appears before a 7 should be 6 to 4 against. The probability should be $\displaystyle\frac{4}{10}$, as indeed it is.
The same argument shows that if E and F are mutually exclusive events of an experiment, then, when independent trials of this experiment are performed, the event E will occur before the event F with probability
$\displaystyle\frac{P(E)}{P(E)+P(F)}$          $\rule[0.02em]{1.0mm}{1.5mm}$