Independent Events 獨立事件

Definition 若下列條件對任意三件事 E, F 和 G 都成立, 則稱 E,F和 G 為獨立事件.

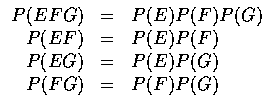
$\begin{array}{rcl} P(EFG)&=&P(E)P(F)P(G) \\ P(EF)&=&P(E)P(F) \\ P(EG)&=&P(E)P(G) \\ P(FG)&=&P(F)P(G) \\ \end{array}$

另外, 當 E,F 和 G 為獨立事件時, 則 E 亦獨立於任何由 F 和 G所組成的事件. 例如, 當E 獨立於 $F\cup G$, 因為

$ \begin{array}{rcl} P[E(F\cup G)]&=& P(EF\cup EG) \\ &=&P(EF)+P(EG)-P(EFG) \\ ... ...E)P(G)-P(E)P(FG) \\ &=&P(E)[P(F)+P(G)-P(FG)] \\ &=&P(E)P(F\cup G) \end{array}$

Of course, we may also extend the definition of independence to more than three events. The events $E_1,E_2,\ldots ,E_n$ are said to be independent if, for every subset $E_{1'},E_{2'},\ldots ,E_{r'}, r\leq n$, of these events

$P(E_{1'}E_{2'}\ldots E_{r'})=P(E_{1'})P(E_{2'})\cdotsP(E_{r'})$
Finally, we define an infinite set of events to be independent if every finite subset of these events is independent.