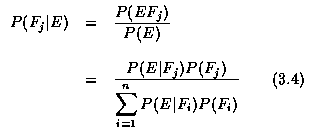Proposition

$\begin{array}{rcl} P(E)&=& P(EF) + P(EF^c) \\ \\ &=& P(E\vert F)P(F) + P(E\ver... ... \\ &=& P(E\vert F)P(F) + P(E\vert F^c)[1-P(F)] \qquad (3.1)\\ \\ \end{array}$
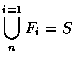
Equation (3.1) may be generalized in the following manner: Suppose that $F_1,F_2,\ldots ,F_n$ are mutually exclusive events such that $\displaystyle\bigcup_n^{i=1}F_i=S$
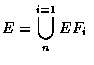In other words, exactly one of the events $F_1,F_2,\ldots ,F_n$ must occur. By writing $\displaystyle E=\bigcup_n^{i=1}EF_i$ and using the fact that the events $EF_i,i=1,\ldots ,n$
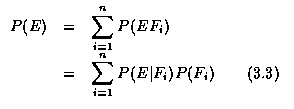
$\begin{array}{rcl} P(E)&=&\displaystyle\sum_{i=1}^n P(EF_i) \\ &=&\displaystyle\sum_{i=1}^n P(E\vert F_i)P(F_i) \qquad (3.3)\\ \end{array}$

Thus Equation (3.3) shows how, for given events $F_1,F_2,\ldots ,F_n$ of which one and only one must occur, we can compute P(E) by first conditioning on which one of the Fi occurs. That is, Equation (3.3) states that P(E) is equal to a weighted average of P(E|Fi), each term being weighted by the probability of the event on which it is conditioned.

Suppose now that E has occurred and we are interested in determining which one of the Fj also occurred. By Equation (3.3), we have the following proposition.

Proposition

$\begin{array}{rcl} P(F_j\vert E)&=&\displaystyle\frac{P(EF_j)}{P(E)} \\ \\ &=&... ...(F_j)}{\displaystyle\sum_{i=1}^n P(E\vert F_i)P(F_i)} \qquad (3.4) \end{array}$
Equation (3.4) is known as Bayes' formula, after the English philosopher Thomas Bayes. If we think of the events Fj as being possible "hypotheses" about some subject matter, then Bayes' formula may be interpreted as showing us how opinions about these hypotheses held before the experiment [that is, the P(Fj)] should be modified by the evidence of the experiment.