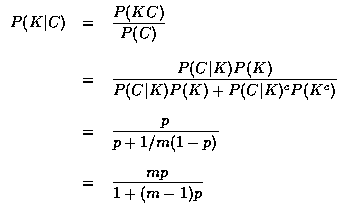Bayes' Formula 貝氏公式

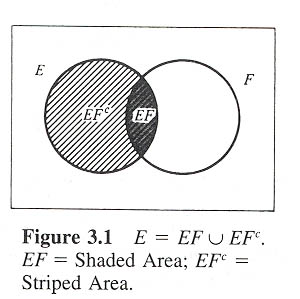
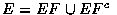
設 E 和 F 為兩事件. 我們可將 E 表示成 $E=EF\cup EF^c$
因為 E 中的點, 必定同時在 E 與 F 中或在 E 但不在 F 中. 如圖:

因 EF 和 EFc 很明顯的是互斥事件, 所以由 Axiom 3 可得

$\begin{array}{rcl} P(E)&=& P(EF) + P(EF^c) \\ \\ &=& P(E\vert F)P(F) + P(E\ver... ... \\ &=& P(E\vert F)P(F) + P(E\vert F^c)[1-P(F)] \qquad (3.1)\\ \\ \end{array}$
Equation (3.1) states that the probability of the event E is a weighted average of the conditional probability of E given that F has occurred and the conditional probability of E given that F has not occurred -- each conditional probability being given as much weight as the event that it is conditioned on has of occurring.

Example
考多重選擇時, 學生可能知道答案, 也可能用猜的. 設學生知道答案的機率為 p, 猜答案的機率為 1-p. 假設學生猜對答案的機率是 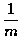$\displaystyle\frac{1}{m}$, 其中, m 為選擇題的選項數. 若學生答對某題, 試求他知道答案的機率為多少?
Solution:
令 C 和 K 分別表示學生答對題目和他確實知道答案的事件, 則
$\begin{array}{rcl} P(K\vert C)&=&\displaystyle\frac{P(KC)}{P(C)}\\ \\ &=&\disp... ...le\frac{p}{p+ 1/m(1-p) } \\ \\ &=&\displaystyle\frac{mp}{1+(m-1)p} \end{array}$
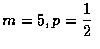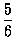因此, 若 $\displaystyle m=5,p=\frac{1}{2}$, 則學生對於他所答對的問題, 確實知道其答案的機率為 $\displaystyle\frac{5}{6}$.          $\rule[0.02em]{1.0mm}{1.5mm}$