The Multiplication Rule 乘法法則
The Multiplication Rule
Proof:
欲證明乘法法則, 祇需要將條件機率的定義應用到等式的右邊就可以了. 亦即
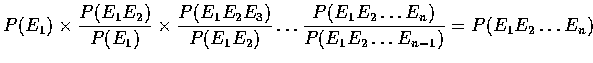
![$\rule[0.02em]{1.0mm}{1.5mm}$](img3.gif)
- Example
- An ordinary deck of 52 playing cards is randomly divided into 4 piles of 13
cards each. Compute the probability that each pile has exactly 1 ace.
- Solution:
- Define events
Ei, i=1,2,3,4 as follows.
E1={ the ace of spades is in any one of the piles }
E2={ the ace of spades and the ace of hearts are in different piles }
E3={ the aces of spades, hearts, and diamonds are all in different piles
}
E4={ all 4 aces are in different piles }
The probability desired is
P(E1E2E3E4) and by the multiplication rule
P(E_1E_2E_3E_4)=P(E_1)P(E_2|E_1)P(E_3|E_1E_2)P(E_4|E_1E_2E_3)
Now, P(E1)=1 since E1 is the sample space S.
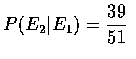 since the pile containing the ace of spades will
receive 12 of the remaining 51 cards.
since the pile containing the ace of spades will
receive 12 of the remaining 51 cards.
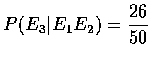 since the piles containing the aces of spades
and hearts will receive 24 of the remaining 50 cards; and finally,
since the piles containing the aces of spades
and hearts will receive 24 of the remaining 50 cards; and finally,
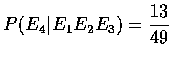 .
.
Therefore, we obtain that the probability that each pile has exactly 1 ace is
That is, there is approximately a 10.5 percent chance that each pile will
contain an ace.
![$\rule[0.02em]{1.0mm}{1.5mm}$](img3.gif)
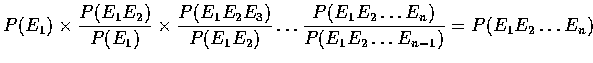
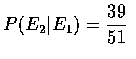 since the pile containing the ace of spades will
receive 12 of the remaining 51 cards.
since the pile containing the ace of spades will
receive 12 of the remaining 51 cards.
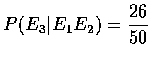 since the piles containing the aces of spades
and hearts will receive 24 of the remaining 50 cards; and finally,
since the piles containing the aces of spades
and hearts will receive 24 of the remaining 50 cards; and finally,
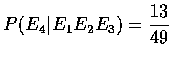 .
.
