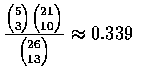Conditional Probabilites 條件機率

假設我們丟兩粒骰子且設 36 種可能結果中每一種結果發生的機會是均等的, 因此每一種結果發生的機率是 $\displaystyle\frac{1}{36}$. 再假設我們觀察到第一粒骰子出現 3, 那麼, 在此條件下, 兩粒骰子的和為 8 的機率是多少呢?

在給定第一粒骰子是 3 的情況下, 我們的試驗最多有六種可能的結果, 即 (3,1) , (3,2) , (3,3) , (3,4) , (3,5) , (3,6). 因為這些可能結果在原來試驗中發生的機率是相等的, 所以這 6 種可能結果仍有相同的發生機率. 也就是說, 給定第一粒骰子是 3, 則 (3,1) , (3,2) , (3,3) , (3,4) , (3,5) , (3,6)等每一結果的(條件)機率都是 $\displaystyle\frac{1}{6}$. 若我們令 E 和 F 分別表示點數和為 8 以及第一粒骰子是 3 的事件 , 那麼剛才 所得到的機率稱為在給予 F 發生的條件下 , 事件 E 發生的條件機率 , 記為 P(E|F)

Definition
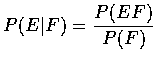
If P(F)>0, then $\displaystyle P(E\vert F)=\frac{P(EF)}{P(F)}$

Example:
袋中有 10 個白色彈珠, 5 個黃色彈珠和 10 個黑色彈珠. 自袋中隨意取出一個彈珠, 且知道它不是黑色的, 試求它是黃色的機率為多少?
Solution:
令 Y 表示彈珠是黃色的事件, 且令 Bc 表示不是黑色的事件. 則
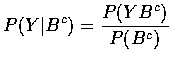
$\displaystyle P(Y\vert B^c)=\frac{P(YB^c)}{P(B^c)}$
所以 YBc = Y. 因此, 在 25 個彈珠有同樣機會被選出的假設下, 我們得
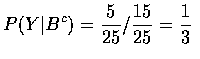
$\displaystyle P(Y\vert B^c) = \frac{5}{25} / \frac{15}{25} = \frac{1}{3}$
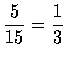值得一提的是我們也可由縮小的樣本空間直接得到此解, 也就是說, 當我們知道取出的彈珠不是黑色時, 此問題變成是求從含有 10 個白色和 5 個黃色彈珠的袋中隨機取出一個黃色彈珠的機率, 很清楚的它是 $\displaystyle\frac{5}{15} = \frac{1}{3}$.          $\rule[0.02em]{1.0mm}{1.5mm}$

Example:
在橋牌遊戲中, 52 張牌平均發給 4 個人 - 稱為 東家, 西家, 北家和南家, 若南北兩家共有 8 張黑桃, 試求東家在剩餘的 5 張黑桃中持有 3 張的機率為多少?
Solution:
求此機率最簡單的方法可能是用縮小的樣本空間. 也就是說, 給予南 - 北家在他們的 26 張牌中有 8 張黑桃後, 剩下的 26 張牌 (其中恰有 5 張黑桃) 要發給東 - 西家. 因為, 每一種發牌法都是機會均等的, 所以東家在他的 13 張牌中恰有 3 張 黑桃的條件機率為
$\displaystyle{{5 \displaystyle\choose 3}{21 \displaystyle\choose 10}\over{26 \displaystyle\choose 13}} \approx 0.339$          $\rule[0.02em]{1.0mm}{1.5mm}$