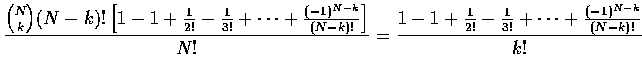The Matching Problem 配對理論
- Example (The Matching Problem)
- Suppose that each of N men at a party throws his hat into the center of the
room. The hats are first mixed up, and then each man randomly selects a hat.
(a) What is the probability that none of the men selects his own hat?
(b) What is the probability that exactly k of the men select their own
hats?
- Solution:
- (a)
We first calculate the complementary probability of at least one man's selecting
his own hat. Let us denote by
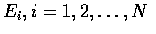 the event that the ith
man selects his own hat. Now,
the event that the ith
man selects his own hat. Now,
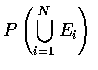 ,
the
probability that at least one of the men selects his own hat, is given by
If we regard the outcome of this experiment as a vector of N numbers, where
the ith element is the number of the hat drawn by the ith man, then there
are N! possible outcomes. [The outcome
,
the
probability that at least one of the men selects his own hat, is given by
If we regard the outcome of this experiment as a vector of N numbers, where
the ith element is the number of the hat drawn by the ith man, then there
are N! possible outcomes. [The outcome
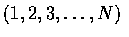 means, for example,
that each man selects his own hat.] Furthermore,
means, for example,
that each man selects his own hat.] Furthermore,
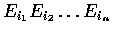 ,
the event that each of the n men
,
the event that each of the n men
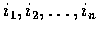 selects his own hat,
can select any of N-n hats, the second can then select any of N-(n+1) hats,
and so on. Hence, assuming that all N! possible outcomes are equally likely,
we see that
Also, as there are
selects his own hat,
can select any of N-n hats, the second can then select any of N-(n+1) hats,
and so on. Hence, assuming that all N! possible outcomes are equally likely,
we see that
Also, as there are
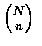 terms in
terms in
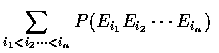 ,
we see that
and thus
Hence the probability that none of the men selects his own hat is
which for N large is approximately equal to
,
we see that
and thus
Hence the probability that none of the men selects his own hat is
which for N large is approximately equal to
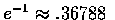 .
In other
words, for N large, the probability that none of the men selects his own hat
is approximately .37.
.
In other
words, for N large, the probability that none of the men selects his own hat
is approximately .37.
(b)
To obtain the probability that exactly k of the N men select their own hats,
we first fix attention on a particular set of k men. The number of ways in
which these and only these k men can select their own hats is equal to the
number of ways in which the other N-k men can select among their hats in such
a way that none of them selects his own hat. But, as
is the probability that not one of N-k men, selecting among their hats,
selects his own, it follows that the number of ways in which the set of men
selecting their own hats corresponds to the set of k men under consideration
is
Hence, as there are
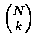 possible selections of a group of k men, it
follows that there are
ways in which exactly k of the men select their own hats. The desired
probability is thus
which for N large is approximately e-1/k!.
possible selections of a group of k men, it
follows that there are
ways in which exactly k of the men select their own hats. The desired
probability is thus
which for N large is approximately e-1/k!.
![$\rule[0.02em]{1.0mm}{1.5mm}$](img19.gif)
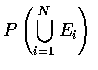 ,
the
probability that at least one of the men selects his own hat, is given by
,
the
probability that at least one of the men selects his own hat, is given by
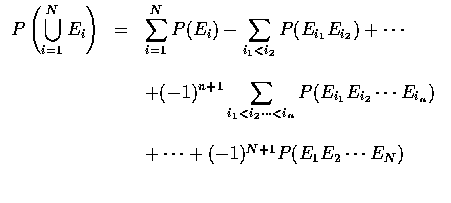
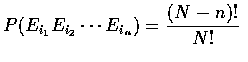
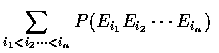 ,
we see that
,
we see that
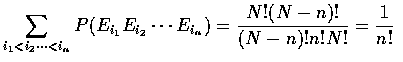
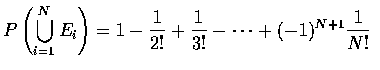
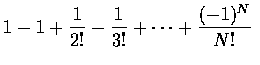
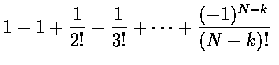
![$\displaystyle(N-k)!\left [1-1+\frac{1}{2!}-\frac{1}{3!}+\cdots +
\frac{(-1)^{N-k}}{(N-k)!}\right ]$](img15.gif)
![$\displaystyle{N\choose k}(N-k)!\left [1-1+\frac{1}{2!}-\frac{1}{3!}+\cdots +
\frac{(-1)^{N-k}}{(N-k)!}\right ]$](img17.gif)