The Birthday Problem 生日問題

Example
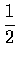If n people are present in a room, what is the probability that no two of them celebrate their birthday on the same day of the year? How large need nbe so that this probability is less then $\displaystyle\frac{1}{2}$?
Solution:
As each person can celebrate his or her birthday on any one of 365 days, there is a total of (365)n possible outcomes. (We are ignoring the possiblity of someone's having been born on February 29.) Assuming that each outcome is equally likely, we see that the desired probability is 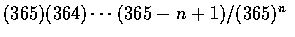$(365)(364)\cdots (365-n+1)/(365)^n$. 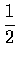It is a rather surprising fact that when n=23, this probability is less then $\displaystyle\frac{1}{2}$. 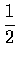That is, if there are 23 people in a room, the probability that at least two of them have the same birthday exceeds $\displaystyle\frac{1}{2}$. Many people find this surprising. Perhaps even more surprising, however, is that this probability increases to .970when there are 50 people in the room. 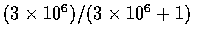And with 100 persons in the room, the odds are better than 3,000,000 to 1 [that is, the probability is greater then $(3\times 10^6)/(3\times 10^6+1)$] that at least two people have the same birthday.          $\rule[0.02em]{1.0mm}{1.5mm}$