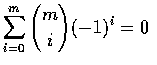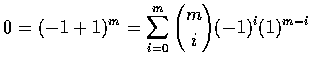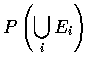 ;
also as this point is contained in
;
also as this point is contained in
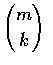 subsets of the type
subsets of the type
Remark
For a noninductive argument for Proposition 4, note first that if a point of
the sample space is not a menber of any of the sets Ei then its probability
does not contribute anything to either side of the equality. On the other hand,
suppose that a point is in exactly m of the events Ei, where m>0. Then
since it is in
![]() its probability is counted once in
its probability is counted once in
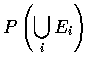 ;
also as this point is contained in
;
also as this point is contained in
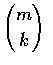 subsets of the type
subsets of the type
![]() ,
its
probability is counted
,
its
probability is counted
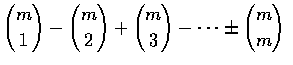
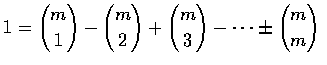
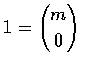 ,
the preceding is equivalent to
,
the preceding is equivalent to