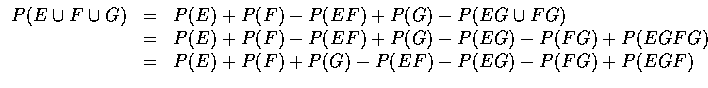Some Simple Propositions
在本節中,我們將提到有關機率的一些簡單命題. 首先, 我們注意到 E 和 Ec永遠是
互斥的, 而且因
![]() ,
所以由 Axiom 2 和 3 得
,
所以由 Axiom 2 和 3 得
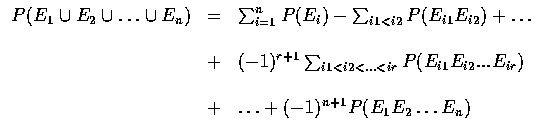
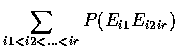 是對集合
是對集合
We may also calculate the probability that any one of the three events E or
F or G occurs:
![]() which by Proposition 3
equals
which by Proposition 3
equals
![]() .
Now it follows from the distributive
law that the events
.
Now it follows from the distributive
law that the events
![]() and
and ![]() are equivalent, and hence we
obtain from the preceding equations that
are equivalent, and hence we
obtain from the preceding equations that