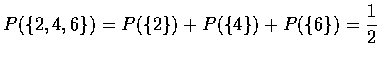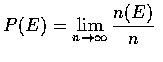
Axioms of Probability 機率公設

One possible way of defining the probability of an event is in terms of its relative frequency. 對樣本空間 S 的每一事件 E, 我們定義 n(E) 為在首 n 次重覆試驗中 事件 E 出現的次數. 則事件 E 的機率 P(E) 定義為

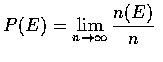
$\displaystyle P(E) = \lim_{n\rightarrow \infty} \frac{n(E)}{n} $

也就是說, 定義 P(E) 為事件 E 發生的(極限)百分比. 因此,它是 E 的極限次數.

考慮一試驗, 其樣本空間為 S. 對樣本空間 S 的每一事件 E, 我們假設 P(E)都有定義且滿足下列三個公設:

Axiom 1
$ 0 \leq P(E) \leq 1 $
Axiom 2
P(S) = 1
Axiom 3
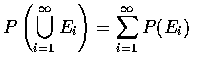對每一互斥事件序列 $ E_1,E_2,\ldots$ (也就是說, 當 $i\neq j$ 時, $E_iE_j=\phi$), $\displaystyle P\left (\bigcup_{i=1}^{\infty} E_i\right ) =\displaystyle\sum_{i=1}^{\infty} P(E_i) $我們稱 P(E) 為事件 E 的機率.

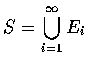若我們考慮一事件序列 $ E_1,E_2,\ldots$, 其中 $E_1=S,E_i=\phi,i>1$, 則因事件彼此互斥且 $\displaystyle S=\bigcup_{i=1}^{\infty}E_i$, 由 Axiom 3 得知

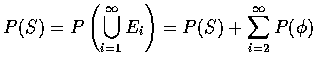
$\displaystyle P(S)=P\left (\bigcup_{i=1}^{\infty} E_i\right ) =P(S)+\displaystyle\sum_{i=2}^{\infty} P(\phi)$

因此, $P(\phi)=0$, 也就是說空事件發生的機率為 0. 又值得一提的是, 對任意有限互斥事件序列 $E_1,E_2,\ldots ,E_n$, 我們有
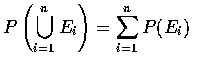
$\displaystyle P\left (\bigcup_{i=1}^n E_i\right) = \displaystyle\sum_{i=1}^n P(E_i)$

只要取 $E_i=\phi,i>n$; 再由 Axiom 3, 即可證得上式.

Example
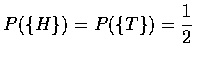
丟一個銅板, 若正, 反面出現的機會相等, 則我們有 $\displaystyle P(\{H\})=P(\{T\})=\frac{1}{2}$
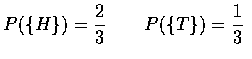
另一方面, 若此銅板是不均勻的, 且我們覺得正面出現的機會為反面的兩倍, 則我們有 $\displaystyle P(\{H\})=\frac{2}{3} \qquad P(\{T\})=\frac{1}{3}$         $\rule[0.02em]{1.0mm}{1.5mm}$

Example
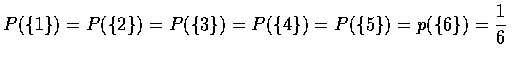丟一骰子, 若六個面出現的機會均等, 則我們有 $\displaystyle P(\{1\})=P(\{2\})=P(\{3\})=P(\{4\})=P(\{5\})=p(\{6\})=\frac{1}{6}$. 由 Axiom 3 可知得偶數點的機率為 $\displaystyle P(\{2,4,6\})=P(\{2\})+P(\{4\})+P(\{6\})=\frac{1}{2}$         $\rule[0.02em]{1.0mm}{1.5mm}$