Commulative, Associative, Distributive and DeMorgan Laws

形成事件之聯集, 交集和餘集的運算遵守某些規則,下面是一些規則:

Commutative laws
交換律 : $E \bigcup F = F \bigcup E$
Associative laws
結合律 : $(E\bigcup F)\bigcup G = E\bigcup (F\bigcup G)$
Distributive laws
分配律 : $(E\bigcup F)\bigcap G = (E\bigcap G)\bigcup (F\bigcap G)$

DeMorgan Law是描述聯集,交集和餘集等三個基本運算間的關係式.

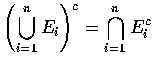
$\displaystyle\left (\bigcup_{i=1}^{n} E_i\right )^c = \bigcap_{i=1}^{n} E_i^c$
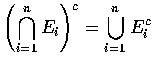
$\displaystyle\left (\bigcap_{i=1}^{n} E_i\right )^c = \bigcup_{i=1}^{n} E_i^c$

Proof:
( $\Rightarrow $)
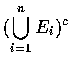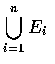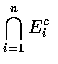首先假設 x 是 $(\displaystyle\bigcup_{i=1}^{n} E_i)^c$ 中的一點, 則 x 不屬於 $\displaystyle\bigcup_{i=1}^{n} E_i$ , 亦即 x 不屬於任何事件 $E_i,i=1,2,\ldots ,n$; 也就是說 x 屬於 $E_i^c,i=1,2,\ldots ,n$; 所以 x 屬於 $\displaystyle\bigcap_{i=1}^n E_i^c$.
( $\Leftarrow $)
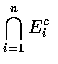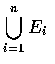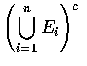假設 x 為 $\displaystyle\bigcap_{i=1}^n E_i^c$ 中的一個點, 則 x 屬於 $E_i^c,i=1,2,\ldots ,n$; 亦即, x 不在 $E_i,i=1,2,\ldots ,n$ 中, 所以 x 不屬於 $\displaystyle\bigcup_{i=1}^{n} E_i$, 也就是說, x 是 $\left (\displaystyle\bigcup_{i=1}^n E_i\right )^c$ 中的一個點.

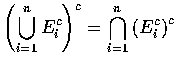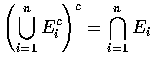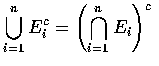
欲證第二個 DeMorgan 法則,可利用第一個法則得 $\left (\displaystyle\bigcup_{i=1}^n E_i^c\right )^c = \displaystyle\bigcap_{i=1}^n\left (E_i^c\right )^c$ 因 (Eic)c = Ei , 故得 $\left (\displaystyle\bigcup_{i=1}^n E_i^c\right )^c = \displaystyle\bigcap_{i=1}^n E_i $再將上式兩邊取餘集便得所要的結果, 即 $\displaystyle\bigcup_{i=1}^n E_i^c =\left (\displaystyle\bigcap_{i=1}^n E_i\right )^c$         $\rule[0.02em]{1.0mm}{1.5mm}$