事件運算法則
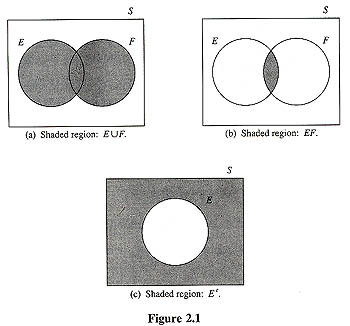
對樣本空間 S 的任兩個事件 E 和 F , 我們定義新事件 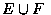 為事件 E和事件 F 的所有點所構成的集合. 也就是說, 當事件 E 或事件 F 發生時,
事件 E
為事件 E和事件 F 的所有點所構成的集合. 也就是說, 當事件 E 或事件 F 發生時,
事件 E 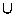 F將會發生. 例如,
F將會發生. 例如,
Union
若 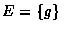 ,
,
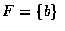 ,
則
,
則
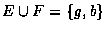 事件
事件 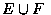 稱為事件 E 和事件 F 的聯集(union).
稱為事件 E 和事件 F 的聯集(union).
Intersection
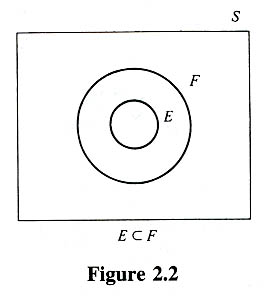
同樣的,我們也可以定義新事件 EF 為事件 E 和事件 F 所共有的點所構成的集合,
稱之為事件 E 和事件 F 的交集(intersection). 也就是說,
僅當事件 E 和事件 F 同時發生時, 事件 EF (有時也寫作 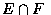 )才會發生.
)才會發生.
Null and Mutually Exclusive
若
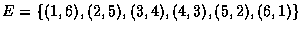 為點數和是 7 的事件,
而
為點數和是 7 的事件,
而
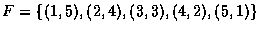 為點數和是 6 的事件,則事件 EF不包含任何的結果, 因此不可能發生. 對這樣的事件, 我們稱它為
空事件(null event) 且以符號
為點數和是 6 的事件,則事件 EF不包含任何的結果, 因此不可能發生. 對這樣的事件, 我們稱它為
空事件(null event) 且以符號 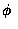 表示之,
若
表示之,
若 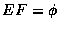 ,則稱 E 和 F 為 互斥事件(mutually exclusive events).
,則稱 E 和 F 為 互斥事件(mutually exclusive events).
我們也可以用類似的方法來定義多於兩個事件的聯集和交集.
若
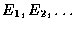 為事件,這些事件的聯集定義為至少屬於某一 En 之所有點所組
成的事件, 其中
為事件,這些事件的聯集定義為至少屬於某一 En 之所有點所組
成的事件, 其中
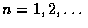 .
以符號
.
以符號
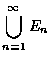 表示此聯集. 同樣, 這些事件 En 的交集定義為每一
表示此聯集. 同樣, 這些事件 En 的交集定義為每一
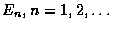 ,
所共有的點所組成的事件,以符號
,
所共有的點所組成的事件,以符號
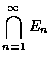 表示.
表示.
- Complement
- 對於每一事件 E, 我們定義一新事件 Ec 為在 S 內但不在 E 中之所有點所
構成的集合, 稱之為 E 的餘事件(complement).
也就是說, Ec 發生若且唯若 E 不發生.
- Contain and Equal
- 對任兩個事件 E 和 F, 若 E 中的所有點也都在 F 內,則我們說 E 包含於 F,
且記為
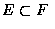 (或
(或
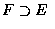 ). 因此, 若
). 因此, 若
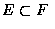 ,
那麼 E 的發生必導致 F 的發生. 若
,
那麼 E 的發生必導致 F 的發生. 若
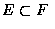 且
且
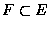 ,
我們說 E 和 F 相等(equal), 且記為 E=F .
,
我們說 E 和 F 相等(equal), 且記為 E=F .
由下圖可以更清楚得了解運算的情形:
![]() 為事件 E和事件 F 的所有點所構成的集合. 也就是說, 當事件 E 或事件 F 發生時,
事件 E
為事件 E和事件 F 的所有點所構成的集合. 也就是說, 當事件 E 或事件 F 發生時,
事件 E ![]() F將會發生. 例如,
F將會發生. 例如,
![]() 為事件,這些事件的聯集定義為至少屬於某一 En 之所有點所組
成的事件, 其中
為事件,這些事件的聯集定義為至少屬於某一 En 之所有點所組
成的事件, 其中
![]() .
以符號
.
以符號
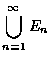 表示此聯集. 同樣, 這些事件 En 的交集定義為每一
表示此聯集. 同樣, 這些事件 En 的交集定義為每一
![]() ,
所共有的點所組成的事件,以符號
,
所共有的點所組成的事件,以符號
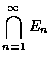 表示.
表示.