On the Distribution of Balls in Urns

如果有 n 個不同的球分配到 r 個不同的箱子中, 則可能的方法有 rn 種. 假如考慮 n 個相同的球, 則可能的分法又如何呢? 以 $(x_1,x_2,\cdots ,x_r)$ 來表示將 n 個相同的球分配到 r 個箱子的可能, 其中 xi 代表在第 i 個箱子中的球數. 則此問題在解 $x_1+x_2+\cdots +x_r=n$之非負的整數解個數.

Proposition 1
There are 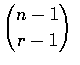$\displaystyle{n-1\choose r-1}$ distinct positive integer-valued vectors $(x_1,x_2,\cdots ,x_4)$ satisfying

$x_1+x_2+\cdots +x_r=n,\qquad x_i>0, i=1,\ldots ,r$

Proposition 2
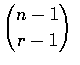There are $\displaystyle{n-1\choose r-1}$ distinct nonnegative integer-valued vectors $(x_1,x_2,\cdots ,x_4)$ satisfying

$x_1+x_2+\cdots +x_r=n, \qquad x_i\geq0, i=1,\ldots ,r$

Example
An investor has 20 thousand dollars to invest among 4 possible investments. Each investment must be in units of a thousand dolars. If the total 20 thousand is to be invested, how many different investment strategies are possible? What if not all the money need be invested?
Solution:
If we let xi, i=1,2,3,4, denote the number of thousands invested in investment number i, then, when all is to be invested, x1,x2,x3,x4 are integers satisfying
$x_1+x_2+x_3+x_4=20, \qquad x_i\geq 0$

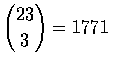Hence, by Proposition 2, there are $\displaystyle{23\choose 3}=1771$ possible investment strategies. If not all of the money need be invested, then, if we let x5denote the amount kept in reserve, a strategy is a nonnegative integer-valued vector (x1,x2,x3,x4) satisfying
$x_1+x_2+x_3+x_4+x_5=20, \qquad x_i\geq 0$

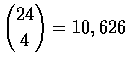Hence, by Proposition 2, there are now $\displaystyle{24\choose 4}=10,626$ possible strategies.          $\rule[0.02em]{1.0mm}{1.5mm}$