If
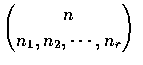 by
by
Multinomial Coefficients 多項式係數
Notation
If
![]() ,
we define
,
we define
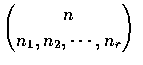 by
by
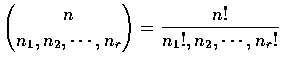
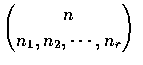 represents the number of possible
divisions of n distinct objects into r distinct group of respective sizes
represents the number of possible
divisions of n distinct objects into r distinct group of respective sizes
The Multinomial Theorem
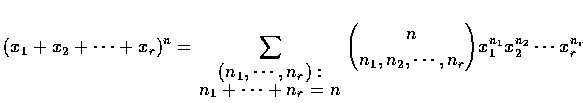
That is, the sum is over all nonnegative integer-valued vectors
![]() such that
such that
![]() .
.
![$\displaystyle\begin{array}{rcl}
(x_1+x_2+x_3)^2&=&{2\choose {2,0,0}}x_1^2x_2^0x...
...2^2+x_3^2+2x_1x_2+2x_1x_3+2x_2x_3
\end{array} \qquad\rule[0.02em]{1.0mm}{1.5mm}$](img7.gif)