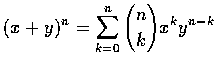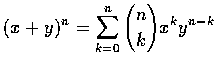 (4.2)
(4.2)
The Binomial Theorem 二項式定理
The Binomial Theorem
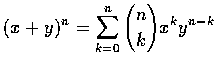 (4.2)
(4.2)
Proof of the Binomial Theorem by Induction:
When n=1, Equation (4.2) reduces to

Assume Equation (4.2) for n-1. Now,

Letting i=k+1 in the first sum and i=k in the second sum, we find that

where the next to last equality follows by Equation (4.1). By induction the
theorem is now proved.
![]()
Combinatorial Proof of the Binomial Theorem:
Consider the product
![]() .
Its expansion consists
of the sum of 2n terms, each term being the product of n factors. Further,
each of the 2n terms in the sum will contain as a factor either xi or
yi for each
i=1,2,...,n. For example,
(x1+y1)(x1+y1)=x1x2+x1y2+y1x2+y1y2 Now, how many of the 2nterms in the sum will have as factors k of the xi's and (n-k) of the
yi's? As each term consisting of k of the xi's and (n-k) of the
yi's corresponds to a choice of a group of k from the n values
x1,x2,...,xn, there are
.
Its expansion consists
of the sum of 2n terms, each term being the product of n factors. Further,
each of the 2n terms in the sum will contain as a factor either xi or
yi for each
i=1,2,...,n. For example,
(x1+y1)(x1+y1)=x1x2+x1y2+y1x2+y1y2 Now, how many of the 2nterms in the sum will have as factors k of the xi's and (n-k) of the
yi's? As each term consisting of k of the xi's and (n-k) of the
yi's corresponds to a choice of a group of k from the n values
x1,x2,...,xn, there are
![]() such terms. Thus, letting
xi=x, yi=y, i=1,...,n, we see that
such terms. Thus, letting
xi=x, yi=y, i=1,...,n, we see that