Combinations 組合

In general, as $n(n-1)\cdots(n-r+1)$ represents the number of different ways that a group of r items could be selected from n items when the order of selection is relevant, and, as each group of r items will be counted r! times in this count, it follows that the number of different groups of r items that could be formed from a set of n items is

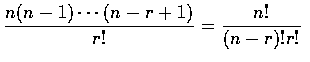
$\displaystyle\frac{n(n-1)\cdots(n-r+1)}{r!}=\frac{n!}{(n-r)!r!}$

Notation and Terminology
We define $\displaystyle{n \choose r}$, for $r\leq n$, by $\displaystyle{n \choose r}=\frac{n!}{(n-r)!r!}$and say that $\displaystyle{n \choose r}$ represents the number of possible combinations of n objects taken r at a time.

Example
A committee of 3 is to be formed from a group of 20 people. How many different committees are possible?
Solution:
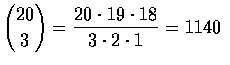There are $\displaystyle{20\choose 3}=\frac{20\cdot 19\cdot 18}{3\cdot 2\cdot 1}=1140$possible committees.          $\rule[0.02em]{1.0mm}{1.5mm}$


A useful combinatorial identity is

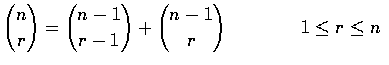
$\displaystyle{n\choose r}={n-1\choose r-1}+{n-1\choose r} \qquad \qquad 1\leq r\leq n$

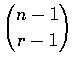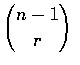Consider a group of n objects and fix attention on some particular one of these objects -- call it object 1. Now, there are $\displaystyle{n-1\choose r-1}$combinations of size r that contain object 1 (since each such combination is formed by selecting r-1 from the remaining n-1 objects). Also, there are $\displaystyle{n-1\choose r}$ combinations of size r that do not contain object 1. As there is a total of $\displaystyle{n \choose r}$ combinations of size r.