We shall now determine the number of permutations of a set of n objects when
certain of the objects are indistinguishable from each other. To set this
straight in our minds, consider the following example. In general, the same
reasoning shows that there are
different permutations of n objects, of which n1 are alike, n2 are
alike, ..., are alike.
- Example
- How many different letter arrangements can be formed using the letters
P E P P E R?
- Solution:
- We first note that there are 6! permutations of the letters
P1 E1 P2 P3 E2 R when the 3 P's and the 2
E's are distinguished from each other. However, consider any one of
these permutations -- for instance,
P1 E1 P2 P3 E2 R. If we now
permute the P's among themselves and the E's among
themselves, then the resultant arrangement would still be of the form
P E P P E R. That is, all 3!2! permutations
are of the form P E P P E R. Hence there are
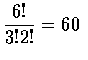 possible letter arrangements of the letters
P E P P E R.
possible letter arrangements of the letters
P E P P E R. 
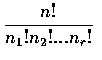
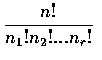
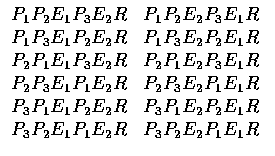
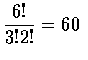 possible letter arrangements of the letters
P E P P E R.
possible letter arrangements of the letters
P E P P E R. ![]()