The Generalized Basic Principle of Counting

The Generalized Basic Principle of Counting
If r experiments that are to be performed are such that the first one may result in any of n1 possible outcomes, and if for each of these n1possible outcomes there are n2 possible outcomes of the second experiment, and if for each of the possible outcomes of the first two experiments there are n3 possible outcomes of the third experiment, and if, ..., then there is a total of 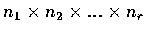$n_1\times n_2\times ... \times n_r$ possible outcomes of the r experiments.

Example
A college planning committee consists of 3 freshmen, 4 sophomores, 5 juniors, and 2 seniors. A subcommittee of 4, consisting of 1 person from each class, is to be chosen. How many different subcommittees are possible?
Solution:
We may regard the choice of a subcommittee as the combined outcome of the four spearate experiments of choosing a single representative from each of the classes. Hence it follows from the generalized version of the basic principle that there are 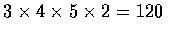$3\times 4\times 5\times 2=120$ possible subcommittees.          $\rule[0.02em]{1.0mm}{1.5mm}$

Example
How many different 7-place license plates are possible if the first 3 places are to be occupied by letters and the final 4 by numbers?
Solution:
By the generalized version of the basic principle the answer is 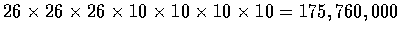$26\times 26\times 26\times 10\times 10\times 10\times 10=175,760,000$.          $\rule[0.02em]{1.0mm}{1.5mm}$