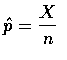 會驅近於常態分佈. 在虛無假設之下,
會驅近於常態分佈. 在虛無假設之下,
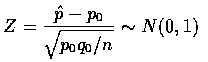 .
又因為對立假設為雙邊假設, 所以在顯著水準為
.
又因為對立假設為雙邊假設, 所以在顯著水準為 Large Sample Tests About p
考慮假設
![]() ,
當試驗次數 n 很大時,
樣本比例為
,
當試驗次數 n 很大時,
樣本比例為
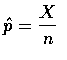 會驅近於常態分佈. 在虛無假設之下,
會驅近於常態分佈. 在虛無假設之下,
![]() approximate
approximate
![]() ,
所以檢定統計量為
,
所以檢定統計量為
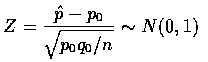 .
又因為對立假設為雙邊假設, 所以在顯著水準為
.
又因為對立假設為雙邊假設, 所以在顯著水準為 ![]() 之下,
棄卻域為
之下,
棄卻域為
![]()
我們想要檢定的假設為
![]() ,
n=400 足夠大,
所以考慮 Z-檢定, 檢定統計量為
,
n=400 足夠大,
所以考慮 Z-檢定, 檢定統計量為
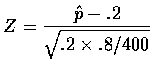 假如考慮顯著水準為
假如考慮顯著水準為
![]() 的情況下, 棄卻域為
的情況下, 棄卻域為
![]() ,而
,而
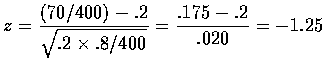
|z|=1.25 小於 1.96, 並沒有落在棄卻域中, 所以在顯著水準為
![]() 之下不考慮棄卻 H0,
也就是這項調查無法給予我們足夠的理由能夠證實貧民戶的比例有所改變.
如果由 P-value 來看,
之下不考慮棄卻 H0,
也就是這項調查無法給予我們足夠的理由能夠證實貧民戶的比例有所改變.
如果由 P-value 來看,
![$\begin{array}{rcl}
\mbox{P-value}&=&P[\vert Z\vert\geq 1.25] \\
&=&P[Z\leq -1.25]+P[Z\geq 1.25] \\
&=&2\times .1056 =.2112 \\
\end{array}$](img13.gif)
也就是說, 在虛無假設如果正確的情況下, 棄卻了 H0 犯錯的機會為 .2112, 所以說因此而棄卻 H0 的理由是相當的薄弱的.