Confidence Interval for p

For large n, a $100(1-\alpha)\%$ confidence interval for p is given by

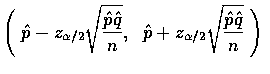
$\displaystyle\Biggl (\;\hat{p}-z_{\alpha/2}\sqrt{\frac{\hat{p}\hat{q}}{n}},\;\; \hat{p}+z_{\alpha/2}\sqrt{\frac{\hat{p}\hat{q}}{n}}\;\Biggr )$

Determining The Sample Size

For $100(1-\alpha)\%$ error margin for the estimation of p, we use the expression $z_{\alpha/2}\sqrt{pq/n}$. The required sample size is obtained by equating $z_{\alpha/2}\sqrt{pq/n}=d$, where d is the specified error margin.

$\displaystyle n=pq\biggl [ \frac{z_{\alpha/2}}{d}\biggl ]^2$

If the value of p is known to be roughly in the neighborhood of a value p*, then n can be determined from

$\displaystyle n=p^*(1-p^*)\biggl [\frac{z_{\alpha/2}}{d}\biggl ]^2$

Without prior knowledge of p, pq can be replaced by its maximum possible value 1/4 and n determined from the relation

$\displaystyle n=\frac{1}{4}\biggl [\frac{z_{\alpha/2}}{d}\biggl ]^2$