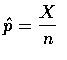 ,
近似於平均數為 p 和標準差為
,
近似於平均數為 p 和標準差為
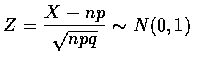
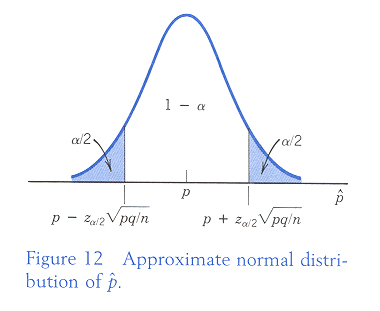
母體比例參數推論
以 p 來表示全體的比例, 當試驗的次數 n 很大時, 我們考慮這樣子的檢定
![]() ,
以 X 表示 n 次的試驗中成功的次數,
則樣本比例即為
,
以 X 表示 n 次的試驗中成功的次數,
則樣本比例即為
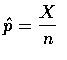 ,
近似於平均數為 p 和標準差為
,
近似於平均數為 p 和標準差為
![]() 的常態分佈. 也就是說, 在虛無假設之下,
的常態分佈. 也就是說, 在虛無假設之下, ![]() 的分配近似於
的分配近似於
![]() ,
因此
,
因此
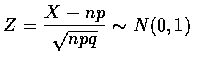
也可以寫成
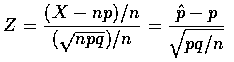
E(X)=np,
![]() ,
因為
,
因為
![]() ,
所以
,
所以
![]() ,
,
![]() .
因此, 我們可以用
.
因此, 我們可以用
![]() 估計母體的比例 p; 用
估計母體的比例 p; 用
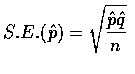 估計母體變異數
估計母體變異數
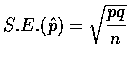 .
.