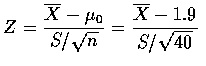
考慮
![]() ,
,
![]() ,
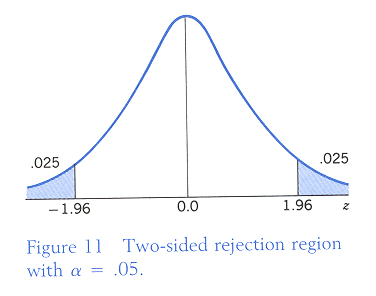
z.025=1.96, 因為為雙邊假設,
所以
,
z.025=1.96, 因為為雙邊假設,
所以
![]()
由前例得知,
![]() ,
s=.475, 由觀察值得到的檢定統計量為
,
s=.475, 由觀察值得到的檢定統計量為
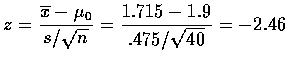
|z|=2.46 > 1.96, 在
如果無法決定 ![]() 是否適當時, 可以考慮 P-value 的值,
是否適當時, 可以考慮 P-value 的值,
![$\begin{array}{rcl}
\mbox{P-value}&=&P[\vert Z\vert\geq 2.46 \\
&=&P[Z\leq -2.46]+P[Z\get 2.46] \\
&=&2\times .0069 =.0138 \\
\end{array}$](img9.gif)
由 P-value 為 .0138 可知, 當有這種觀察值時棄卻虛無假設 H0犯錯的機率相當的小, 所以仍維持棄卻 H0, 且有足夠的理由說明支持 H1 的對立假設.
接著我們來看看雙邊假設檢定以及 P-value 的問題.
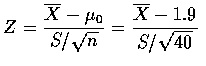
考慮
![]() ,
,
![]() ,
z.025=1.96, 因為為雙邊假設,
所以
,
z.025=1.96, 因為為雙邊假設,
所以
![]()

由前例得知,
![]() ,
s=.475, 由觀察值得到的檢定統計量為
,
s=.475, 由觀察值得到的檢定統計量為
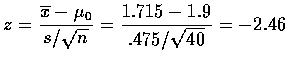
如果無法決定 ![]() 是否適當時, 可以考慮 P-value 的值,
是否適當時, 可以考慮 P-value 的值,
![$\begin{array}{rcl}
\mbox{P-value}&=&P[\vert Z\vert\geq 2.46 \\
&=&P[Z\leq -2.46]+P[Z\get 2.46] \\
&=&2\times .0069 =.0138 \\
\end{array}$](img9.gif)
由 P-value 為 .0138 可知, 當有這種觀察值時棄卻虛無假設 H0犯錯的機率相當的小, 所以仍維持棄卻 H0, 且有足夠的理由說明支持 H1 的對立假設.