前面我們希望能夠在較小 ![]() 之下, 也就是說犯錯的機率很小, 取得棄卻的機率,
但另一方面, 我們也不希望型二誤差
之下, 也就是說犯錯的機率很小, 取得棄卻的機率,
但另一方面, 我們也不希望型二誤差 ![]() 太大.
太大.
![]() when
when ![]() (H0 true)
(H0 true)
![]() when
when ![]() (H1 true)
(H1 true)
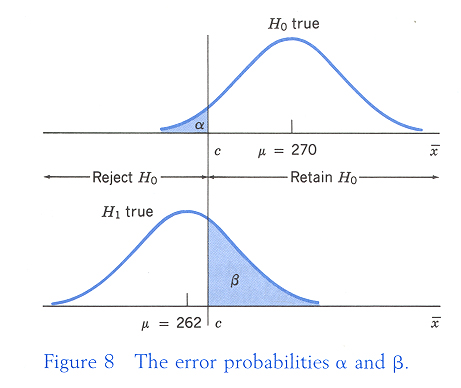
下圖可以看出 ![]() 與
與 ![]() 之間的關係, 將
之間的關係, 將 ![]() 視為一個未知的變數,
在不同的假設下得到的棄卻域 RR, 相對的可以找出
視為一個未知的變數,
在不同的假設下得到的棄卻域 RR, 相對的可以找出 ![]() ,
在 H1 正確的情形下,
不支持 H1 犯錯的機率. 對於相同的
,
在 H1 正確的情形下,
不支持 H1 犯錯的機率. 對於相同的 ![]() ,
可以借由增加樣本數 n 來降低
,
可以借由增加樣本數 n 來降低 ![]() .
.
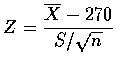 ,
考慮顯著水準 2.5%, 則
,
考慮顯著水準 2.5%, 則
當觀察到
![]() ,
s=22, 則
,
s=22, 則
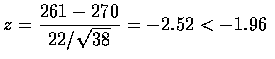 ,
所以在
,
所以在
![]() 的情況下有相當的信心棄卻 H0.
的情況下有相當的信心棄卻 H0.