在上一章中我們有約略提到有關利用樣本變異數來估計母體變異數的想法, 而在上一節中我們可以發現當樣本數 n 很大的時候, 信賴區間的估計式就可以寫成這樣,

Estimate $\pm$(z-value)(estimated standard error)
所以當母體變異數未知, n 足夠大時, 考慮用樣本變異數 S 來取代母體變異數.

Large Sample Confidence Interval for $\mu$

When n is large, a $100(1-\alpha)\%$ confidence interval for $\mu$ is given by

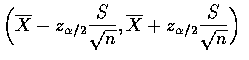
$\displaystyle\biggl( \overline{X}-z_{\alpha/2}\frac{S}{\sqrt{n}}, \overline{X}+z_{\alpha/2}\frac{S}{\sqrt{n}}\biggr )$

where S is the sample standard deviation.

例
估計某大城市中, 餐廳男女服務生每個星期的平均收入, 由 75 位餐館工作人員中取樣, 平均值與標準差分別為 $227 和 $15, 試求每週 平均收入 (a) 90% 及 (b) 80% 信賴區間.

$n=75, \overline{x}=227, s=15$

(a)
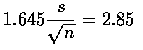$1-\alpha=.90$, 所以 $\alpha/2=.05$, $z_{\alpha/2}=1.645$, $\displaystyle1.645\frac{s}{\sqrt{n}}=2.85$.

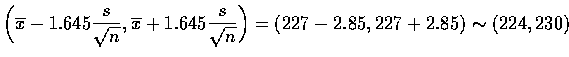
$\displaystyle\biggl (\overline{x}-1.645\frac{s}{\sqrt{n}}, \overline{x}+1.645\frac{s}{\sqrt{n}}\biggr ) =(227-2.85, 227+2.85)\sim(224,230)$

這是說在調查者中有 90% 的信心相信平均收入 $\mu$ 是在 $224 至 $230 之間. 即在 75 位中的隨機樣本有 90% 產生包含 $\mu$ 的區間 $\overline{x}\pm1.64s/\sqrt{n}$.

(b)
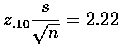$1-\alpha=.80$, 所以 $\alpha/2=.10$, $z_{\alpha/2}=1.28$, $\displaystyle z_{.10}\frac{s}{\sqrt{n}}=2.22$. 因此, 對於 $\mu$ 的 80% 信賴區間為 $(227-2.22, 227+2.22)\sim(225,229)$, 80% 的信賴區間比 90% 的信賴區間要短, 較短的區間似乎給予 $\mu$ 較正確的位置, 但長期重覆下函蓋 $\mu$ 正確的次數則較少.