Confidence Interval 信賴區間

令 X1,...,Xn 是一隨機樣本且 $\mu$ 是一個未知的母體參數, 而 $\mu$ 的信賴區間是由樣本觀察值 X1,...,Xn 計算得之的一區間, 以 (L,U) 表示, 使得抽樣能有較高的機會會落於真正的母體參數附近. 這個機會稱為 level of confidence.

令 $(1-\alpha)\%$ 是給定的高機率, 而 L 和 U 是 X1,...,Xn 的函數. 若 $P[L<\mu<U]=1-\alpha$ 的區間 (L,U) 稱為參數 $\mu$ 的一個 $100(1-\alpha\%)$的信賴區間, 且 $(1-\alpha)$ 稱為此區間的信賴度(level of confidence).

對 $\overline{X}$ 而言, 我們有

$\displaystyle P\biggl [\mu-1.96\frac{\sigma}{\sqrt{n}}<\overline{X}< \mu+1.96\frac{\sigma}{\sqrt{n}}\biggr ]=.95$

而下面兩項事件是等價的,

1.
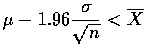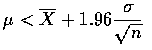
$\displaystyle\mu-1.96\frac{\sigma}{\sqrt{n}}<\overline{X}$ 等於 $\displaystyle\mu<\overline{X}+1.96\frac{\sigma}{\sqrt{n}}$
2.
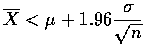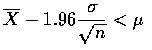
$\displaystyle\overline{X}<\mu+1.96\frac{\sigma}{\sqrt{n}}$ 等於 $\displaystyle\overline{X}-1.96\frac{\sigma}{\sqrt{n}}<\mu$
所以下面的兩個式子也是等價的,
$\displaystyle\biggl [ \mu-1.96+\frac{\sigma}{\sqrt{n}}<\overline{X}< \mu+1.96\frac{\sigma}{\sqrt{n}} \biggr ]$
與
$\displaystyle\biggl [ \overline{X}-1.96+\frac{\sigma}{\sqrt{n}}<\mu< \overline{X}+1.96\frac{\sigma}{\sqrt{n}} \biggr ]$

上面的事件是說 $(\overline{X}-\mu)$ 落於 $-1.96\sigma/\sqrt{n}$ 及 $1.96\sigma/\sqrt{n}$. 因此, 機率如下,

$\displaystyle P\biggl [\mu-1.96\frac{\sigma}{\sqrt{n}}<\overline{X}< \mu+1.96\frac{\sigma}{\sqrt{n}}\biggr ]=.95$

亦可寫做

$\displaystyle P\biggl [ \overline{X}-1.96\frac{\sigma}{\sqrt{n}}<\mu< \overline{X}+1.96\frac{\sigma}{\sqrt{n}}\biggr ] =.95$

上面兩個式子看起來似乎也是等價的, 但可能有不同的解釋, 第二個式子說明了, 在抽樣之前, $\overline{X}-1.96\sigma/\sqrt{n}$ 至 $\overline{X}+1.96\sigma/\sqrt{n}$ 將涵蓋未知母體參數的機率為 .95. 當母體為常態, $\sigma$ 已知時,

$(\overline{x}-1.96\sigma/\sqrt{n}, \overline{x}+1.96\sigma/\sqrt{n})$

稱為 對於 $\mu$ 95% 的信賴區間 (95% confidentce interval for $\mu$).