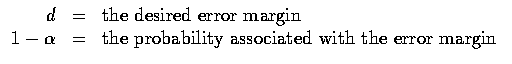
所以在
Determining the sample size
這節要介紹的是, 當我們給定了誤差範圍想要得到給定的機率時, 所需要的抽樣的樣本數 n 是我們所關心的, 有效樣本數少的話可以節省成本付出.
首先我們先定義或是說給定誤差範圍及滿足的誤差的機會,
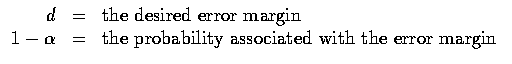
所以在
![]() 的誤差機會下,
的誤差機會下,
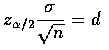
![$\displaystyle n=\biggl [ z_{\alpha/2}\frac{\sigma}{d} \biggr ]^2$](img4.gif)
To be
![]() sure that the error of estimation
sure that the error of estimation
![]() does not exceed d, the required sample size is
does not exceed d, the required sample size is
![$\displaystyle n=\biggl [ z_{\alpha/2}\frac{\sigma}{d} \biggr ]^2$](img4.gif)
If ![]() is completely unknow, a small-scale preliminary sampling is
necessary to obtain an estimate of
is completely unknow, a small-scale preliminary sampling is
necessary to obtain an estimate of ![]() to be used in the formula to
compute n.
to be used in the formula to
compute n.