接著介紹一個常見的符號, 樣本變異數(sample variance) S, 當無法得知母體的變異數時, 我們可以考慮用樣本變異數來取代, 換句話說, 利用 sample variance estimate population variance, 當 n 很大的時候, 利用 $S/\sqrt{n}$ 來估計 $\sigma/\sqrt{n}$ 的誤差影響將變得不重要.

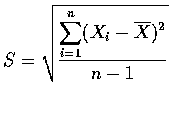
$\displaystyle S=\sqrt{\displaystyle\frac{\displaystyle\sum_{i=1}^{n}(X_i-\overline{X})^2}{n-1}}$

Point Estimation of the Mean
Parameter: Population mean $\mu$.
Data: X1,...,Xn (a random sample of size n)
Estimator: $\overline{X}$ (sample mean)
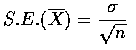$\displaystyle S.E.(\overline{X})=\frac{\sigma}{\sqrt{n}}$,
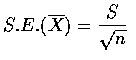
estimated $\displaystyle S.E.(\overline{X})=\frac{S}{\sqrt{n}}$
For large n, the $100(1-\alpha)\%$ error margin is $z_{\alpha/2}\sigma/\sqrt{n}$. (If $\sigma$ is unknown, use S in place of $\sigma$.)

例
接續前面提過松苗例子, 詳列資料如下, 單位:公分

$\begin{array}{cccccccc} \hline 2.6&1.9&1.8&1.6&1.4&2.2&1.2&1.6 \\ 1.6&1.5&1.4&... ...8&1.7&0.8&1.5&2.0&2.2 \\ 1.5&1.6&2.2&2.1&3.1&1.7&1.7&1.2 \\ \hline \end{array}$

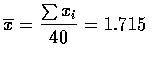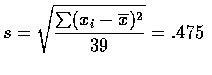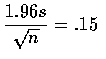則 $\displaystyle\overline{x}=\frac{\sum{x_i}}{40}=1.715$, $\displaystyle s=\sqrt{\frac{\sum(x_i-\overline{x})^2}{39}}=.475$假如想要找 95% 誤差範圍, $1-\alpha=.95$, $\alpha/2=.025$, $z_{\alpha/2}=1.96$. 因此, $\displaystyle\frac{1.96s}{\sqrt{n}}=.15$ 公分. 所以, 我們可以得知平均樹苗的高度為 1.715, 而有 95% 的機率會涵蓋 $\pm .15$ 之間.