Ponit Estimation of A Population Mean
首先, 我們先來看點估計的問題, 因為我們對於母體的某一個未知的參數(或稱為母數) 有興趣, 比如說母體平均數, 可以利用上一章所提到的 statistic.
A statistic intended for estimating a parameter is called a point estimator, or simply an estimator. The standard deviation of an estimator is called its standard error: S.E.
例如我們前一章中提到的, 樣本平均數(sample mean)
![]() 以及
母體平均數(population mean)
以及
母體平均數(population mean) ![]() 之間的關係, 便可以用來做為點估計.
之間的關係, 便可以用來做為點估計.
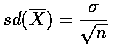 so
so
當然, 當 n 很大的時候, 我們可以說 "
![]() 可以用來估計
可以用來估計 ![]() ",
但我們希望知道到底需要多少的 n, 或是 n 多大時
",
但我們希望知道到底需要多少的 n, 或是 n 多大時
![]() 有多少可能機會會涵蓋
有多少可能機會會涵蓋 ![]() .
我們知道, 變異數與 n 有關, 控制 n 的大小,
可以控制變異數的大小, 然後可以得到我們想要的.
.
我們知道, 變異數與 n 有關, 控制 n 的大小,
可以控制變異數的大小, 然後可以得到我們想要的.
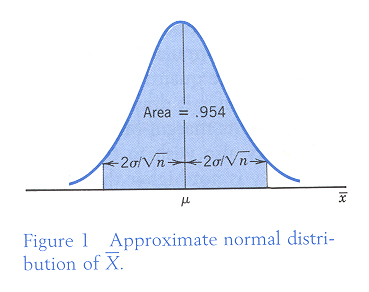
由上圖中, 可以知道
![]() 用來估計
用來估計 ![]() ,
在
,
在
![]() 的區域內,
的區域內,
![]() 可能會有 95.4%
的機會涵蓋
可能會有 95.4%
的機會涵蓋 ![]() .
.