- (a)
- If a random sample of size 64 is selected, what is the probability that the sample mean will lie between 80.8 and 83.2?
- (b)
- With a random sample of size 100, what is the probability that the sample mean will lie between 80.8 and 83.2?
- (a)
- We have
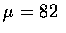 and
and 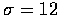 .
Since n=64 is large, the central
limit theorem tells us that the distribution of
.
Since n=64 is large, the central
limit theorem tells us that the distribution of
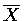 is approximately
normal with
is approximately
normal with
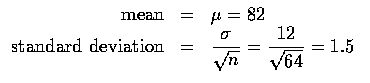
To calculate
![$P[80.8<\overline{X}<83.2]$](img6.gif) ,
we convert to the standardized
variable
,
we convert to the standardized
variable
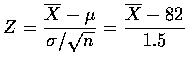
The z-values corresponding to 80.8 and 83.2 are
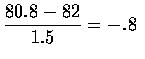 and
and
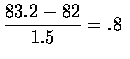
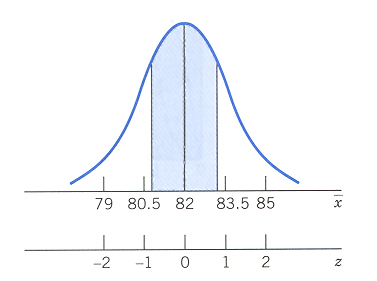
Consequently,
![$\begin{array}{rcl}
P[80.8<\overline{X}<83.2]&=&P[-.8<Z<.8] \\
&=& .7881-.2119 \mbox{ (using the normal table) } \\
&=&.5762 \\
\end{array}$](img10.gif)
- (b)
- We now have n=100, so
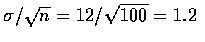 ,and
,and
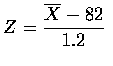
Therefore,
![$\begin{array}{rcl}
P[80.8<\overline{X}<83.2]&=&\displaystyle P[\frac{80.8-82}{1...
...-82}{1.2}] \\
&=&P[-1.0<Z<1.0] \\
&=&.8413-.1587 \\
&=&.6826 \\
\end{array}$](img13.gif)
Note that the interval (80.8, 83.2) is centered at
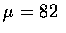 .
The probability
that
.
The probability
that
 will lie in this interval is larger for n=100 than for
n=64.
will lie in this interval is larger for n=100 than for
n=64.