$\overline{X}$ is normal when sampling from a normal population

In random sampling from a normal population with mean $\mu$ and stadard deviation $\sigma$, the sample mean $\overline{X}$ has the normal distribution with mean $\mu$ and standard deviation $\sigma /\sqrt{n}$.

When sampling from a nonnormal population, the distribution of $\overline{X}$depends on the particular form of the population distribution that prevails. A surprising result, known as the central limit theorem, states that when the sample size n is large, the distribution of $\overline{X}$ is approximately normal, regardless of the shape of the population distribution. In practice, the normal approximation is usually adequate when n is greater than 30.

Central Limit Theorem

Whatever the population, the distribution of $\overline{X}$ is approximately normal when n is large.
In random sampling from an arbitrary population with mean $\mu$ and standard deviation $\sigma$, when n is large, the distribution of $\overline{X}$ is approximately normal with mean $\mu$ and standard deviation $\sigma /\sqrt{n}$. Consequently,

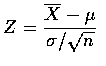$\displaystyle Z=\frac{\overline{X}-\mu}{\sigma /\sqrt{n}}$ is approximately N(0,1)