Distribution of The Sample Mean
上一節中, 我們看到了樣本平均數
![]() 的分配情形,
接著我們想知道此分配的期望值與變異數, 也就是說母體有母體本身的分配,
而由母體抽樣出來的樣本有自己的分配, 稱為抽樣分配. 而一般而言,
母體的期望值及變異數, 甚至分配我們可能均無法得知, 所以只好利用抽樣來估計.
的分配情形,
接著我們想知道此分配的期望值與變異數, 也就是說母體有母體本身的分配,
而由母體抽樣出來的樣本有自己的分配, 稱為抽樣分配. 而一般而言,
母體的期望值及變異數, 甚至分配我們可能均無法得知, 所以只好利用抽樣來估計.
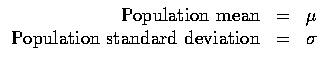
Mean and Standard Deviation of
![]()
The distribution of the sample mean, based on a random sample of size n, has
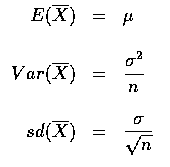
![]() 的抽樣分配是以母體平均數
的抽樣分配是以母體平均數 ![]() 為中心的分配,
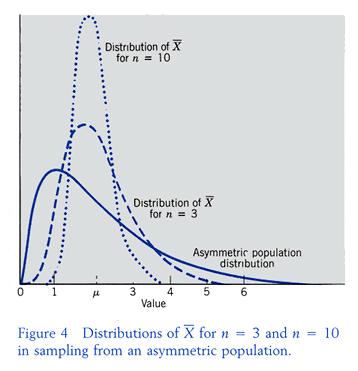
不受抽樣的樣本數多少所影響, 但變異數會受樣本數影響, 當樣本數 n 增加時,
變異愈小, 愈精確, 抽樣分配將會近似母體分配, 分配圖型會近似母體分配
為中心的分配,
不受抽樣的樣本數多少所影響, 但變異數會受樣本數影響, 當樣本數 n 增加時,
變異愈小, 愈精確, 抽樣分配將會近似母體分配, 分配圖型會近似母體分配