首先先看看隨機變數 X 的分配
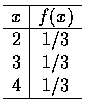
再來, X1 與 X2 都是由上述的母體中抽出, 屬於相同分配且相互獨立,
(x1,x2) 可能的抽樣值如下, 以
![]() 表示
表示
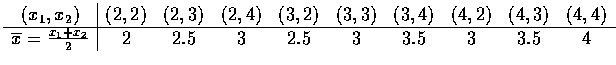
上述每一種出現的機率相等均為
![]() ,
所以可以求得
,
所以可以求得
![]() 的分配情況, 如下.
的分配情況, 如下.
The Porbability Distribution
of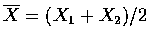
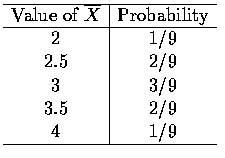
of

Sampling Distribution 抽樣分配
首先先看看隨機變數 X 的分配
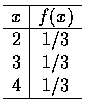
再來, X1 與 X2 都是由上述的母體中抽出, 屬於相同分配且相互獨立,
(x1,x2) 可能的抽樣值如下, 以
![]() 表示
表示
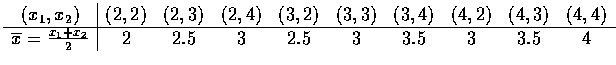
上述每一種出現的機率相等均為
![]() ,
所以可以求得
,
所以可以求得
![]() 的分配情況, 如下.
的分配情況, 如下.
