The normal approximation to the binomial applies when n is large and the success probability p is not too close to 0 or 1. The binomial probability of $[a\leq X\leq b]$ is approximated by the normal probability of $[a-\frac{1}{2}\leq X\leq b+\frac{1}{2}]$.

When np and n(1-p) are both large, say, greater than 15, the binomial distribution is well approximated by the normal distribution having $\mbox{mean}=np$ and $\mbox{sd}=\sqrt{np(1-p)}$. That is,

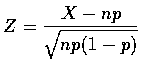$\displaystyle Z=\frac{X-np}{\sqrt{np(1-p)}}$ is approximately N(0,1)

例
有一長達五年抽樣調查的資料顯示有 30% 的成年人有長期飲用含有酒精成份的飲料. 假如現在仍然維持這樣子的比例, 則請問在 1000 位成年人當中, 長期飲用含有酒精成份飲料的人數 (a) 小於 280 位, (b) 大於等於 316 位, 的機率分別為多少?

假設隨機變數 X 為 1000 位成年人中長期飲運含有酒精成份飲料的人數. 則在所占比例 30% 的假設下, X 為 n=1000,p=.3 的二項分配, 也就是說 $X\sim B(1000, .3)$, 因此

$np=300, \sqrt{np(1-p)}=\sqrt{210}=14.49$

意思是說 X 的分配趨近於 N(300,14.49).

(a)
X<280 和 $X\leq 279$ 的意思是一樣的, 在連續較正項之下

$\begin{array}{rcl} P[X\leq 279]&\approx&\displaystyle P[Z\leq\frac{279.5-300}{14.49}] \\ \\ &=&P[Z\leq -1.415] \\ \\ &=&.0786 \\ \\ \end{array}$
(b)
$\begin{array}{rcl} P[X\geq 316]&\approx&\displaystyle P[Z\geq\frac{315.5-300}{14.49}] \\ \\ &=&P[Z\geq -1.07] \\ \\ &=&1-.8577=.1423 \\ \\ \end{array}$