現在我們來考慮用常態分配來逼近二項分配, 原因在於, 當二項分配 B(n,p) 的 n很大的時候, 計算它的機率值將是一件不容易的事. 但我們知道在 $X\sim B(n,p)$ 中, P[X=x] 是有值的(不為 0), 但在 $X\sim N(0,1)$ 中, P[X=x] 是沒有太大意義的. 所以我們考慮用連續校正項 continuity correction 來計算機率, 也就是考慮, 在 $X\sim N(0,1)$ 中 $P[x-\frac{1}{2}\leq X\leq x+\frac{1}{2}]$ 的值來逼近.

For n=15 and p=.4, the binomial distribution assigns P[X=7]=.177 that

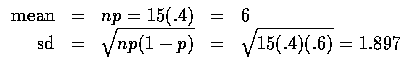
$\begin{array}{rcccl} \mbox{mean}&=&np=15(.4)&=&6 \\ \mbox{sd}&=&\sqrt{np(1-p)}&=&\sqrt{15(.4)(.6)}=1.897 \\ \end{array}$

To obtain an approximation, we select the normal distribution with the same mean ,$\mu = 6$, and same $\sigma =1.897$. The normal approximation is then the probability assigned to the interval $7-\frac{1}{2}$ to $7+\frac{1}{2}$.

$\begin{array}{rcl} P[6.5<X<7.5]&=&P[\displaystyle\frac{6.5-6}{1.897}<\frac{X-6}... ...7.5-6}{1.897}] \\ \\ &\approx&P[.264<Z<.791]=.7855-.6041=.1814 \\ \end{array}$