Standard Normal Distribution 標準常態分配

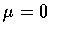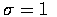
The standard normal distribution has a bell-shaped density with mean $\mu = 0$ and standard deviation $\sigma = 1$

The standard normal distribution is denoted by N(0,1) or Z.

1.
$P[Z \leq 0]=.5$
2.
$P[Z \leq - z]=1-P[Z\leq z]=P[Z\geq z]$

標準常態分配的值可以由查標準常態分配表得知.

例
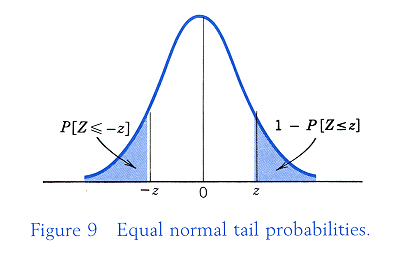
Find $P[Z<-1.9 \mbox{ or } Z>2.1]$.
The two events [Z<-1.9] and [Z>2.1] are incompatible, so we add their probabilities: $P[Z<-1.9 \mbox{ or } Z>2.1]=P[Z<-1.9]+P[Z>2.1]$. As indicated in follow, P[Z>2.1] is the area to the right of 2.1, which is $1-[\mbox{Area to left of }2.1]=1-.9821=.0179$. The normal table gives P[Z<-1.9]=.0287 directly. Adding these two quantities, we get $P[Z<-1.9 \mbox{ or } Z>2.1]=.0287+.0179=.0466$