二項分配 Binomial Distribution

投擲一銅板 4 次, 正面代表成功(S), 反面代表失敗(F), 則最後可能就有 $2\times 2\times 2\times 2=16$ 種不同的結果. 可以看成重複 4 次白努力試驗. 假如現在為 n 次試驗, 每次成功的機率為 p, 我們可以考慮隨機變數 X, 代表試驗成功的次數. 則稱 X 的機率分配稱為具有 n 次試驗且成功的機率為 p的二項分配. X 的可能值為 0,1,2,3,...,n. 以 $X\sim B(n,p)$ 表示.

直觀上, 二項分配 B(n,p) 可以視為由 n 個 Bernoulli 分配組成, Bernoulli 分配是 n=1 二項分配的特例. 以 B(p) 或 B(1,p) 表示.

A probability model is an assumed form of the probability distribution that describes the chance behavior for a random variable X. Probabilities are expressed in terms of relevant population quantities, called the parameters.

The Binomial Distribution
Denote

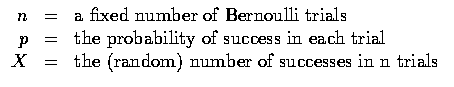
$\begin{array}{rcl} n&=&\mbox{a fixed number of Bernoulli trials} \\ p&=&\mbox{... ...al} \\ X&=&\mbox{the (random) number of successes in n trials} \\ \end{array}$

The random variable X is called a binomial random variable. Its distribution is called a binomial distribution.