Consider a lot (population) of items in which each item can be classified as either defective or nondefective. Suppose that a lot consists of 15 items, of which 5 are defective and 10 are nondefective. Do the conditions for Bernoulli trials apply when sampling (1) with replacement and (2) without replacement?
- 1
- Sampling with replacement
An item is drawn at random (i.e., in a manner that all items in the lot are equally likely to be selected). The quality of the item is recorded and it is returned to the lot before the next drawing. The conditions for Bernoulli trials are satisfied. If the occurrence of a defective is labeled S, we have P(S)=5/15. - 2
- Sampling without replacement
In situation (1), suppose that 3 items are drawn one at a time but without replacement. Then the condition concerning the independence of trials is violated. For the first drawing, P(S)=5/15. If the first draw produces S, the lot then consists of 14 items, 4 of which are defective. Given this information about the result of the first draw, the conditional probability of obtaining an S on the second draw is then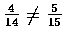
,
which establishes the lack of independence.
This violation of the condition of independence loses its thrust when the
population is vast and only a small fraction of it is sampled. Consider sampling
3 items without replacement from a lot of 1500 items, 500 of which are defective
. With S1 denoting the occurrence of an S in the first draw and S2 that
in the second, we have
and
.
For most practicl purposes, the latter fraction can be approximated by 5/15. Strictly speaking, there has been a violation of the independence of trials, but it is to such a negligible extent that the model of Bernoulli trials can be assumed as a good approximation.