The mean of a random variable X is also called its expected value and, alternatively, denoted by E(X). That is, the mean $\mu$ and expected value E(X) are the same quantity and will be used interchangeably. The mean of X or population mean

$\begin{array}{rcl} E(X)&=&\mu \\ &=&\sum(\mbox{value}\times\mbox{probability})=\sum x_if(x_i) \end{array}$

Here the sum extends over all the distinct values xi of X.

例
假如有一旅遊保險公司提供旅客在旅遊時的財物意外損失險, 保險金額為 $1000, 而在 200 個旅遊人次中約僅有 1 件發生意外, 則該公司所提供的保險服務需收取多少的保費才算合理.

首先, 保險公司可能付出 $ 1000 的機率為 1/200=.005, 接著我們以隨機變數 X來表示保戶可能收到的保費. 如下,

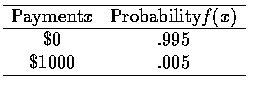
$\begin{array}{cc} \hline \mbox{Payment} x&\mbox{Probability} f(x) \\ \hline \$ 0 &.995 \\ \$ 1000 & .005 \\ \hline \end{array}$

所以我們可以得到

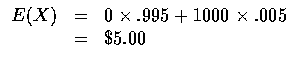
$\begin{array}{rcl} E(X)&=&0\times .995 + 1000 \times .005 \\ &=&\$ 5.00 \\ \end{array}$

也就是說, 公司所提出的這個保險辦法, 其保費應該為 $ 5 才是合理的. 如果旅客需要這項服務, 接受這項保險, 則需要繳 $ 5, 這個例子說明了期望值的意義.