Note:
機率分配在統計推論的假設:

例
假設有一小森林中有 30% 的樹受到某種寄生細菌的感染. 現在隨機選取出 4 棵樹, 令 X 為受到寄生細菌感染樹的數目, 則 X 可能的情況如下, (I) 表示受感染, (N) 表示無感染.

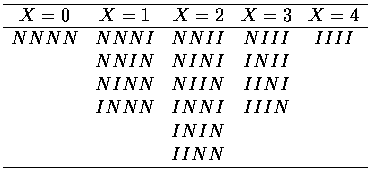
$\begin{array}{ccccc} \hline X=0 &X=1 &X=2 &X=3 &X=4 \\ \hline NNNN&NNNI&NNII&NI... ...NI& \\ &INNN&INNI&IIIN& \\ & &ININ& & \\ & &IINN& & \\ \hline \end{array}$

因為隨機選取的 4 棵樹, 每一棵樹都有可能為"受感染"或是"無感染"等 2 種情況, 所以 4 棵數就總共有 $2\times 2\times 2\times 2=16$ 種可能的組合情況. 而整個森林的樹受感染的比例為 30%, 所以 P(I)=.3 而 P(N)=.7. 接下來我們就可以計算 $P(NNNN)=.7\times .7\times .7\times .7\times = .2401$, 所以 P[X=0]=.2401. 而事件[X=1] 有 4 種組合狀況, 因為每一種組合都含有 1 個 I, 3 個 N, 每種狀況的機率相同, 為 $P(NNNI)=(.7)^3\times (.3)=.1029$, 因此 $P[X=1]=4\times .1029=.4116$.
同理可推

$\begin{array}{rcll} P[X=2] & = & 6\times (.7)^2\times (.3)^2 & = .2646 \\ P[X=... ...s (.7)\times (.3)^3 & = .0756 \\ P[X=4] & = & (.3)^4 = .0081 & \\ \end{array}$

The Proability Distribution of X
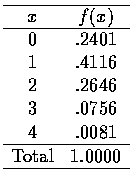
$\begin{array}{cc} \hline x&f(x) \\ \hline 0&.2401 \\ 1&.4116 \\ 2&.2646 \\ 3&.0756 \\ 4&.0081 \\ \hline \mbox{Total}&1.0000 \\ \hline \end{array}$

事件 $[X \geq 2]$ 是由 [X=2], [X=3], [X=4] 所組成的. 同理也可以求得事件 $[X \leq 2]$ 的機率. 因此事件 $[X \geq 2]$ 的機率即為,

$\begin{array}{rcl} P[X \leq 2]&=&f(2)+f(3)+f(4) \\ &=&.2646+.0756+.0081 \\ \end{array}$