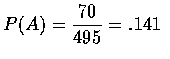有限樣本隨機抽樣
The Rule of Combinations
Notation:
從 n 個不同的物品中選取 r 個物品的可能組合方法, 稱為
"從 n 中選取 r 個的組合方法數".
The number of possible choices of r objects from a group of
N distinct objects is denoted by
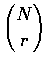 ,
which reads as
"N choose r".
,
which reads as
"N choose r".
Formula:
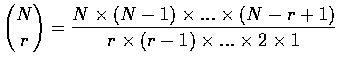
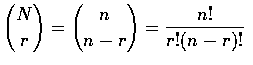
A sample of size n selected from a population of N distinct objects is said
to be a random sample if each collection of size n has the same
probability
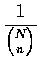 of being selected.
of being selected.
- 例
- 現由 12 人中選出 4 人組成一個研究小組. 而在這 12 人中分別有 5 人屬於
A 部門, 7 人屬於 B 部門. 請問
- (a)
- 由這 12 人中任取 4 人組成研究小組, 有幾種方法.
- (b)
- 1 人必須為 B 部門, 3 人為 A 部門, 則有幾種方法.
- (c)
- 如果是隨機選取的, 則選取得 1 人由 B, 3 人由 A
選出的機率為何.
- 解:
- (a)
- 12 人中任取 4 人, 有
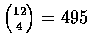 方法.
方法.
- (b)
- 1 人取自 B 部門, 有
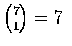 方法. 3 人取至 A
部門, 有
方法. 3 人取至 A
部門, 有
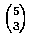 方法.
方法.
所有, 總共為
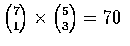 選取的方法
選取的方法
- (c)
- 隨機由 495 種可能的方式中, 選取 70 種可能的方式,
則機率為
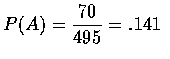
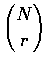 ,
which reads as
"N choose r".
,
which reads as
"N choose r".
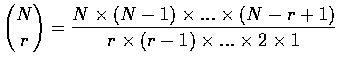
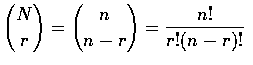
![]() of being selected.
of being selected.