A是互斥事件
![]() 的聯集,
的聯集,
![]() .
.
![]()
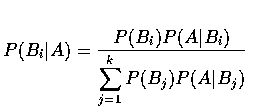
where
![]()
Bayes Theorem 貝氏定理
首先, 試驗者注意到原先 B1, B2,...,Bk 的幾種可能的敘述, 但並不確知其中何者發生. 例如, 對一位藥理學家而言, 對兩項不知道的藥品可能其中一個成份要比另一個有效或者無效; 對一個廣告代理商而言, 在一項展示中他們以各種顏色組合可能有效. 根據關於一些狀況或由相似狀況所得的實驗證據的敘述, 試驗者可以做一些機率 P(B1),P(B2),...,P(Bk) 的評估,反映他的感覺, 當作各種不同的原始敘述發生的可能. 此類的稱為原先敘述的事前機率 (prior probabilities). 現在, 試驗者以觀察及試驗的方法收集資料, 我們記為 A. 試驗者在已知觀察某一特定的原先敘述 Bj 之條件下則可決定實驗 A的機率. 即是條件機率 P(A|Bj), j=1,...,k. 依貝氏定理, 試驗者可計算條件機率 P(Bj|A), j=1,...,k, 沒有其他關於觀察試驗之後不同的原先敘述其修正的表示法要比這些來得好. 這些修正後的機率稱為事後機率 (posterior probabilities); 為試驗者想對原先未知敘述的推論基礎.
A是互斥事件
![]() 的聯集,
的聯集,
![]() .
.
![]()
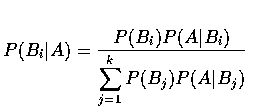
where
![]()