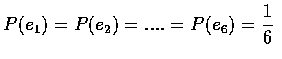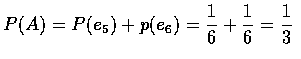No Title

事件的機率

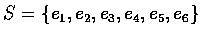考慮投擲一個公平的骰子所可能的結果, 分別為 1,2,3,4,5,6, 6面出現的可能性都相等, 樣本空間為 $S=\{e_1,e_2,e_3,e_4,e_5,e_6\}$ , 則各別元素的機率為

$\displaystyle P(e_1)=P(e_2)=....=P(e_6)=\frac{1}{6}$

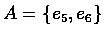, outcome equally likely. 稱為 uniform probability model 假設事件 A 為表示投擲點數大於 4 的事件, 則 $A=\{e_5,e_6\}$ ,

$\displaystyle P(A)=P(e_5)+p(e_6)=\frac{1}{6} + \frac{1}{6}=\frac{1}{3}$

When the elementary outcomes are modeled as equally likely, we have a uniform probability model. If there are k elementary outcomes in S, eachis assigned the probability of 1/k.
An event A consisting of m elementary outcomes is then assigned
$\displaystyle P(A)=\frac{m}{k}= \frac{\mbox{No. of elementary outcomes in} A} {\mbox{No. of elementary outcomes in} S}$