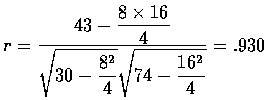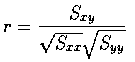
where
若有 n 個成對的觀察值 (x,y), 則 r 的求法如下:
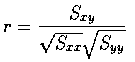
where
![]() the sum of cross products of the
x deviations with the y deviations
the sum of cross products of the
x deviations with the y deviations
![]() the sum of squared deviations of x
the sum of squared deviations of x
![]() the sum of squared deviations of y
the sum of squared deviations of y
由上面的公式及下表可以求得相關係數
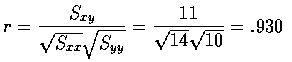 說明了 (x,y) 有高度的相關性.
說明了 (x,y) 有高度的相關性.

另可用下列方式求得,
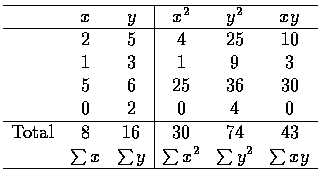
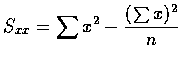 ,
,
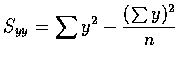 ,
,
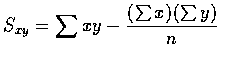 ,
,